Summarize this article:
 1048 Learners
1048 LearnersLast updated on August 5, 2025
Square root of 20

The square root of 20 is a value “y” such that when “y” is multiplied by itself → y ⤫ y, the result is 20. The number 20 has a unique non-negative square root, called the principal square root.

What Is the Square Root of 20?
The square root of 20 is ±4.47213595. Finding the square root is just the inverse of squaring a number and hence, squaring 4.47213595 will result in 20.
The square root of 20 is written as √20 in radical form, where the ‘√’ sign is called the “radical” sign. In exponential form, it is written as (20)1/2

Finding the Square Root of 20
We can find the square root of 20 through various methods. They are:
- Prime factorization method
- Long division method
- Approximation/Estimation method

Square Root of 20 By Prime Factorization Method
The prime factorization of 20 is done by dividing 20 by prime numbers and continuing to divide the quotients until they can’t be separated anymore.
- Find the prime factors of 20.
- After factorizing 20, make pairs out of the factors to get the square root.
- If there exist numbers that cannot be made pairs further, we place those numbers with a “radical” sign along with the obtained pairs.
So, Prime factorization of 20 = 2 × 2 × 5
But here in the case of 20, a pair of factor 2 can be obtained and a single 5 is the remaining
So, it can be expressed as √20 = 2√5.
2√5 is called the simplest radical form of √20
Explore Our Programs



Square Root of 20 By Long Division Method
This method is used for obtaining the square root for non-perfect squares, mainly. It usually involves the division of the dividend by the divisor, getting a quotient and a remainder too sometimes.
Follow the steps to calculate the square root of 20:
Step 1: Write the number 20, and draw a bar above the pair of digits from right to left.
Step 2: Now, find the greatest number whose square is less than or equal to. Here, it is
4, Because 42=16 < 20
Step 3: Now divide 20 by 4 such that we get 4 as quotient and then multiply the divisor with the quotient, we get 16.
Step 4: Add a decimal point after the quotient 4, and bring down two zeroes and place it beside the difference 4 to make it 400.
Step 5: Add 4 to same divisor, 4. We get 8.
Step 6: Now choose a number such that when placed at the end of 8, a 2-digit number will be formed. Multiply that particular number by the resultant number to get a number less than 400. Here, that number is 4.
84×4=336<400.
Step 7: Subtract 400-336=64. Again, bring down two zeroes and make 64 as 6400. Simultaneously add the unit’s place digit of 84, i.e., 4 with 84. We get here, 88. Apply Step 5 again and again until you reach 0.
We will show two places of precision here, and so, we are left with the remainder, 1216 (refer to the picture), after some iterations and keeping the division till here, at this point
Step 8 : The quotient obtained is the square root. In this case, it is 4.472….

Square Root of 20 By Approximation
Estimation of square root is not the exact square root, but it is an estimate.
Here, through this method, an approximate value of square root is found by guessing.
Follow the steps below:
Step 1: Find the nearest perfect square number to 20. Here, it is 16 and 25.
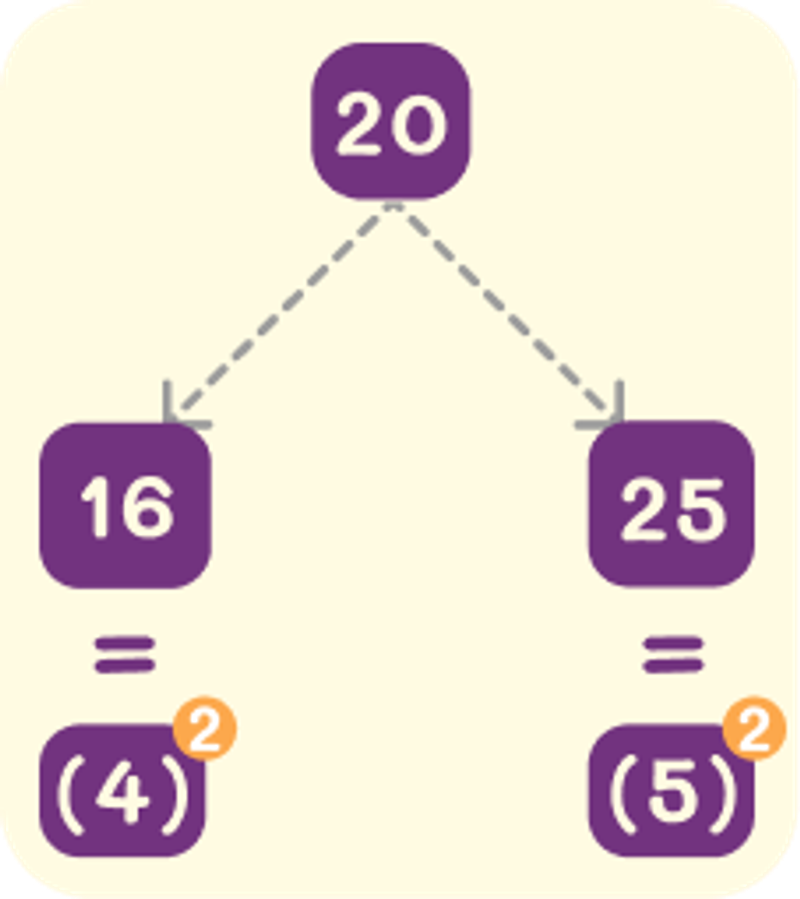
Step 2: We know that, √16=4 and √25=5. This implies that √20 lies between 4 and 5.
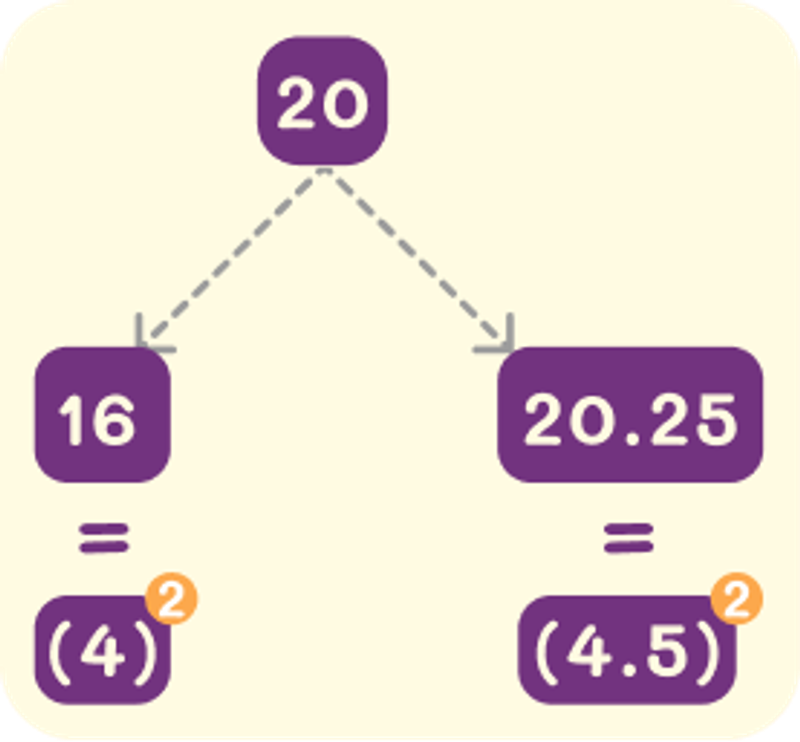
Step 3: Now we need to check √20 is closer to 4 or 5. Let us consider 4 and 4.5. Since (4)2=16 and (4.5)2=20.25. Thus, √20 lies between 4 and 4.5.
.png?updatedAt=1727343351989)
Step 4: Again considering precisely, we see that √20 lies close to (4.5)2=20.25. Find squares of (4.2)2=17.64 and (4.49)2= 20.16.
We can iterate the process and check between the squares of 4.4 and 4.48 and so on.
We observe that √20=4.472…

Common Mistakes and How to Avoid Them in the Square Root of 20
When we find the square root of 20, we often make some key mistakes, especially when we solve problems related to that. So, let’s see some common mistakes and their solutions

Square Root of 20 Examples

Problem 1
If x= √20, what is x²-5 ?

x= √20
⇒ x2 = 20
⇒ x2-5 = 20-5
⇒ x2-5 = 15
Answer : 15
Explanation
we did the square of the given value of x and then subtracted 5 from it.

Problem 2
Find the length of a side of a square whose area is 20 cm²

Given, the area = 20 cm2
We know that, (side of a square)2 = area of square
Or, (side of a square)2 = 20
Or, (side of a square)= √20
Or, side of a square = ±4.4721.
But, the length of a square is a positive quantity only, so, the length of the side is 4.4721 cm.
Answer: 4.4721 cm
Explanation
We know that, (side of a square)2 = area of square.
Here, we are given with the area of the square, so, we can easily find out its square root because its
Square root is the measure of the side of the square.

Problem 3
Simplify (√20 + √20) ⤫ √20

(√20 + √20) × √20
= (4.4721 + 4.4721) × 4.4721
= 8.9442 × 4.4721
= 39.9993
Answer: 39.9993
Explanation
We first solved the part inside the brackets, i.e., √20 + √20, which resulted into 8.9442 and then multiplying it with √20
which is 4.4721.we get 39.9993

Problem 4
If y=√20, find y²

firstly, y=√20= 4.47213595
Now, squaring y, we get,
y2= (4.47213595)2=20
or, y2=20
Answer : 20
Explanation
squaring “y” which is same as finding the square value of √20 resulted to 20.

Problem 5
Calculate (√20/4 + √20/2)

√20/4 + √20/2
= 4.47213595/4 + 4.47213595/2
= 1.11803399 + 2.236067
=3.354101
Answer: 3.354101
Explanation
From the given expression, we first found the value of square root of 20 then solved by simple divisions and then
simple addition.


FAQs on 20 Square Root
1.Is the square root of 20 a real number?
2.Is 20 a perfect square or a non-perfect square?
3.Is the square root of 20 a rational or irrational number?
4.√20 falls between which perfect squares?
5.How do I find the square root of 20 manually?

Important Glossaries for Square Root of 20
Exponential form:An algebraic expression that includes an exponent. It is a way of expressing the numbers raised to some power of their factors. It includes continuous multiplication involving base and exponent.
Example: 2 ⤬ 2 ⤬ 2 ⤬ 2 = 16
Or, 24 = 16, where 2 is the base, 4 is the exponent
Prime Factorization: Expressing the given expression as a product of its factors
Example: 48=2 ⤬ 2 ⤬ 2 ⤬ 2 ⤬ 3
Prime Numbers:Numbers which are greater than 1, having only 2 factors as →1 and Itself. Ex: 1,3,5,7,....
Rational numbers and Irrational numbers:The Number which can be expressed as p/q, where p and q are integers and q not equal to 0 are called Rational numbers. Numbers which cannot be expressed as p/q, where p and q are integers and q not equal to 0 are called Irrational numbers.
Perfect and non-perfect square numbers:Perfect square numbers are those numbers whose square roots do not
include decimal places. Ex: 4,9,25 Non-perfect square numbers are those numbers whose square roots comprise decimal places. Ex :3, 8, 24



Jaskaran Singh Saluja
About the Author
Jaskaran Singh Saluja is a math wizard with nearly three years of experience as a math teacher. His expertise is in algebra, so he can make algebra classes interesting by turning tricky equations into simple puzzles.
Fun Fact
: He loves to play the quiz with kids through algebra to make kids love it.



























