Geometric Sequence

A geometric sequence is a list of numbers, where each term is obtained by multiplying the previous term by a constant called the common ratio. If r > 1, the sequence grows; if 0 < r < 1, it decreases. Real-life examples include population growth or scientific experiments.

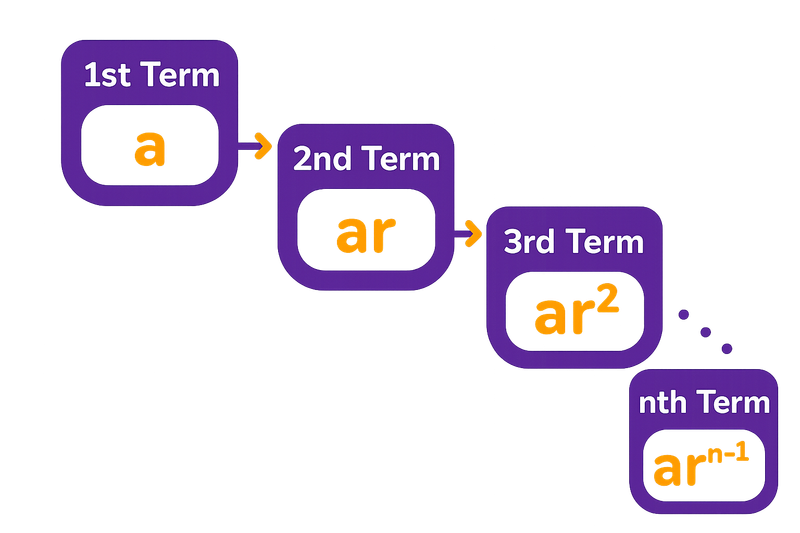
Examples of Geometric Sequences
 

• 2, 4, 8, 16, 32, …. These are increasing geometric sequences. The first term a is 2, and the common ratio, r, is 2. Each term is double the previous one. 
   
• 100, 50, 25, 12.5, … in this sequence, a = 100 and r = \(\frac{1}{2}\). Each term is half of the previous one; hence, it is a decreasing geometric sequence. 
   
• 3, -6, 12, -24, … This is an example of an alternating geometric sequence. Here, the common ratio r = -2, which causes the signs of each term to alternate. 
  
   

Based on the number of terms a sequence has, geometric sequences are of two types. They are: 
 

• Finite geometric sequences
   
• Infinite geometric sequences. 
   

Finite geometric sequence

A finite geometric sequence has a limited number of terms. It has a clear beginning and end. The geometric sequence 5, 10, 20, 40 is an example of a finite geometric sequence. 


Infinite geometric sequence 

An infinite geometric sequence has an infinite number of terms and continues indefinitely. For example, 1, \(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{4}\), …….

A geometric sequence is a chain of numbers in which every term is obtained by multiplying the previous term by a fixed number, known as the common ratio.

1. nth Term of a Geometric Sequence


 \(a_n = a_1 \times r^{\,n-1}\)


Where, 

a_n= the nth term
‘
a = first term

r = common ratio

n = term number

2. Sum of the First n Terms (Finite Sum)


\(S_n = \frac{a_1 (1 - r^n)}{1 - r}, \quad \text{for } r \neq 1\)

Where, 
 

\(S_n\)​ = sum of first n terms

a = first term

r = common ratio

n  = number of terms

 

3. Sum to Infinity (Infinite Geometric Series)

 

\(S_\infty = \frac{a_1}{1 - r}, \quad \text{for } |r| < 1\)

Where, 
 

S∞​ = infinite sum 

a = first term

r = common ratio (must be between 1< r < 1)

A geometric sequence is calculated by multiplying the previous one by a fixed number, known as the common ratio. The nth term formula is:

\(a_n = a_1 \times r^{\,n-1}\)


Where:

 

a_n = the nth term

a = the first term of the sequence

r  = the common ratio

n = the position of the term in the sequence

A recursive formula says that every term in a sequence is based on its preceding term(s). In a geometric sequence, every term is obtained by multiplying the previous term by a fixed number known as the common ratio. The recursive formula is:

\(a_n = r \times a_{n-1}, \quad \text{for } n \ge 2\)

Where:

a_n​ = the nth term

a_n-1 ​ = the previous term


r  = the common ratio
 

You must also specify the first term: a_1​

Example: If a₁ = 2 and r = 3, then the sequence is:



2, 6, 18, 54, …


Recursive formula:

a₁ = 2

\(a_n = a_{n-1} \times 0.3, \quad \text{for } n > 1\)

The formula for the sum S_n ​of the first n terms of a finite geometric sequence is:


\(S_n = \frac{a(1 - r^n)}{1 - r}, \quad \text{for } r \neq 1\)


Where:

 

a₁ is the first term,

r is the common ratio between consecutive terms?

n is the number of terms to sum?

If the common ratio r = 1, the series becomes a constant sequence, and the sum is simply:


S_n= n × a

Derivation


To derive this formula, consider the geometric series:


\(S_n = a + a r + a r^2 + a r^3 + \dots + a r^{\,n-1} \)


Multiply both sides by the common ratio (r):


\(r S_n = a r + a r^2 + a r^3 + \dots + a r^n\)


Subtract the original series from this new equation:


\(r S_n - S_n = \bigl(a r + a r^2 + a r^3 + \dots + a r^n \bigr) - \bigl(a + a r + a r^2 + \dots + a r^{\,n-1} \bigr)\)


Simplifying the right-hand side:


\((r - 1) S_n = a r^n - a\)


Solving for Sn 


\(S_n = \frac{a(1 - r^n)}{1 - r}, \quad \text{for } r \neq 1\)


 

Example: Consider a geometric series with the first term a = 4, the common ratio r = 3, and n = 6 terms.


Given: First term a = 4
 

Common ratio r = 3

Number of terms n = 6


Using the formula: \(S_6 = 4 \times \frac{1 - 3^6}{1 - 3}\)



First, calculate 3⁶:


\(3^6 = 729\)


Now, we will substitute into the formula:


\(S_6 = 4 \times \frac{1 - 729}{1 - 3} = 4 \times \frac{-728}{-2}\)


\(S_6 = 4 \times 364 = 1456\)


The answer is 1456.

An infinite geometric series is a sum of terms, where each term is multiplied by the same common ratio (r) to get the next one.

The sum exists only if the absolute value of the ratio is less than 1 (|r| < 1).

 

Formula: \(S_\infty = \frac{a}{1 - r}, \quad \text{for } |r| < 1\)



Where:

 

a = first term

r = common ratio

If |r| ≥ 1, the series doesn’t have a finite sum (it diverges).

 

Example:


Series:\( 2 + 1 +\frac{1}{2} + \frac{1}{4} + \frac{1}{3} + …\)


a = 2

r = \(\frac{1}{2}\)

\(S_\infty = \frac{2}{1 - ½} = \frac{2}{½} = 4\)


The sum of the series is 4.
 

Geometric sequences are number patterns where each term is obtained by multiplying the previous term by a constant ratio. With the right tips and tricks, you can quickly find terms, calculate sums, and solve problems efficiently without getting lost in lengthy calculations.


 

• Always remember that negative ratios produce alternating sequences. Use absolute value to track magnitude, handle sign separately. Fractional ratios decrease the sequence toward 0. Useful in finance (depreciation, discounting).

• Many sequences use powers of numbers (2, 3, 10, etc.), which can help you calculate terms faster without a calculator.

• When n is large, express terms in powers rather than expanding them.

• If the common ratio is negative, the sequence alternates signs. Track the magnitude and sign separately to avoid errors.
  
   
• Divide any term by its previous term to find the common ratio. This helps you spot the pattern fast and avoid mistakes.
  
   
• Parents and teachers should encourage students to identify the first term (a) and the common ratio (r) before solving geometric sequence problems. This will give them clarity and prevent them from getting confused with arithmetic sequences. 

• Use real-life contexts such as population growth, compound interest, or so on, to help students understand why geometric sequences increase or decrease rapidly. 

• Parents and teachers can demonstrate geometric sequences by repeatedly folding paper or doubling objects, making the concept more visual and engaging for learners. 

• Encourage students to compare two consecutive terms by division to verify the common ratio. This will help them confirm whether a sequence is geometric. 

• Have students estimate the sizes of terms in a geometric sequence before calculating them. It will build their number sense and help with easy calculation.

A geometric sequence is a pattern where each term is obtained by multiplying the previous term by a constant ratio. This concept is not just theoretical—it appears in many real-world scenarios:

 

Robotics: The lengths or angles of robotic arm segments can increase geometrically to reach higher points efficiently, with each segment following a fixed ratio for smooth motion.

Architecture: Architects often use geometric sequences when designing structures like spiral staircases or tiered platforms. The height and width of each step or level can follow a geometric pattern to ensure balance and aesthetics.

Art and Design: Artists use geometric sequences to create perspective and depth in drawings or designs. Objects may decrease in size geometrically as they appear further away, creating realistic visual effects.

Finance: Geometric sequences appear in compound interest calculations. Each term represents the total amount after successive periods, where the amount grows by a fixed ratio each time.

Engineering: The sizes of structural elements, like steps in a staircase or layers in a tower, can follow a geometric sequence to maintain balance, safety, and proper load distribution.