Pre Algebra

Pre-algebra is an introductory branch of mathematics that builds the foundation for Algebra 1 and Algebra 2. The topics include factors, multiples, ratios, exponents, order of operations, number theory, probability, mean, median, and mode. 

Pre-algebra is an important concept in mathematics that helps in building a strong foundation for higher-level algebra. The main concepts in pre-algebra include:
 

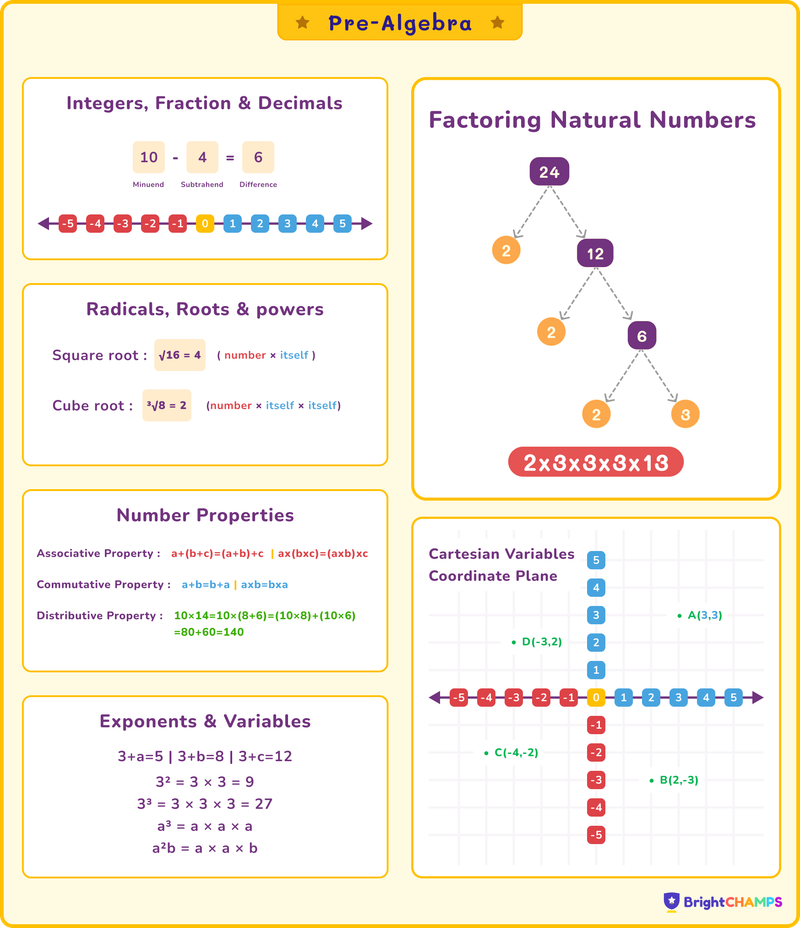
Number Theory 

 

• Whole Numbers: A whole number is a number that starts from 0 and goes on without any fractions or decimals. Whole numbers are always non-negative. For example, 0,1,2,3,4,5,6,…
  
   
• Roman Numerals: Roman numerals are a number system that originated in ancient Rome. Instead of digits like 1, 2, 3, it uses letters from the Latin alphabet to represent numbers.
  
   
• Integers: Integers are a set of numbers that include all whole numbers, their negative counterparts, and zero. In simple words, integers are numbers without fractions or decimals that can be positive, negative, or zero. The set of integers is: …,−3,−2,−1,0,1,2,3,…
  
   
• Rational Numbers: A rational number is any number that can be written in the form \(\frac{p}{q}\), where, \(p\) and \(q\) are integers and \(q ≠ 0\). For example, \(\frac{1}{2}\),\(\frac{-3}{6}\), \(5\), \(0\), \(\frac{7}{1}\) are all rational numbers.
  
   
• Real Numbers: Real numbers are all the numbers that can be found on the number line.
  They include whole numbers, integers, fractions, decimals, rational numbers, and irrational numbers, basically, every number you can think of, except imaginary numbers like \( \sqrt{-1} \).
  
   
• Absolute Value: The absolute value of a number is its distance from 0 on the number line, without considering its sign. In simple terms, it makes every number positive (or zero). It is denoted by |x|. For example, |5| = 5 is the distance of 5 from 0. 
   

Factors and Multiples 

 

• Factors: Factors are numbers that you can multiply together to get another number. For example, factors of 6 are: 1 × 6 = 6, 2 × 3 = 6, Therefor, factors of 6 are 1, 2, 3 and 6.
  
   
• Multiples: A multiple of a number is what you get when you multiply that number by 1, 2, 3, 4… and so on. For example, multiples of 3 are 3, 6, 9, 12, 15, etc. 
  
   
• Prime numbers and composite numbers: A prime number is a number greater than 1 that has exactly two factors: 1 and itself. And a composite number is a number greater than 1 that has more than two factors. For example, 2, 3, 5, 7, 11, etc. are prime numbers and 4, 6, 8, 9, etc. are composite numbers. 
  
   
• Prime factorization: Prime factorization is the process of breaking a number into its prime factors, the prime numbers that multiply together to give the original number. 12 ÷ 2 = 6 → 2, 6 ÷ 2 = 3 → 2, 3 ÷ 3 = 1 → 3. So the prime factorization of is 12 = 2 × 2 × 3 or 2² × 3.
  
   

Ratio and Proportion

 

• Ratio: A ratio is a way to compare two or more quantities. It tells us how much of one thing there is compared to another. It shows the relationship between numbers. Furthermore, it is usually written as a : b (read as a to b). For example, 2:3. 
  
   
• Proportion: A proportion is an equation that shows two ratios are equal. In simple words, When two ratios are the same, they are in proportion. It is usually written as \(\frac{a}{b}=\frac{c}{d}\) or \(a:b=c:d\). 

Exponents and Square Roots

 

• Fractions: A fraction represents a part of a whole. If you divide something into equal parts, a fraction tells how many parts we have. It is written in the form: \(\frac{numerator}{denominator}\). 
  
   
• Exponents: An exponent tells us how many times a number (the base) is multiplied by itself. It is written as aⁿ, where a is the base (the number being multiplied) and n is the exponent (how many times to multiply). For example, 23=2×2×2=8. 
  
   
• Order of Operations: The Order of Operations is a set of rules that tells us which calculations to do first in a math expression. The basic rules of operations are (BODMAS / PEMDAS).
  
   
• Square root: A square root of a number is a value that, when multiplied by itself, gives the original number. It is denoted by the symbol \(\sqrt{} \). If \(x ^2=y\), then \(x=\sqrt{y} \). for example, \(\sqrt{16}=4 \).

Statistics 

 

• Mean, Median, Mode: The mean is the sum of all numbers divided by how many numbers there are. The median is the middle number when the numbers are arranged in order. The mode is the number that appears most frequently.
  
   
• Probability: Probability is the chance of an event happening. It tells us how likely something is to occur. Examples of probability are tossing a coin, rolling a die, etc.  

Pre-algebra introduces important formulas that help students in solving a wide range of mathematical problems. Some important formulas related to pre-algebra are:

• Speed = \(\frac{Distance}{Time}\)

• Pythagoras Theorem: \(c^2 = a^2 + b^2\), where a and b are two sides of a right-angled triangle and c is the hypotenuse. 

• Profit = Selling price - Cost price

• Loss = Cost price - Selling price

• Profit percentage = \(\frac{Profit}{Cost price}  × 100\)

• Loss percentage = \(\frac{Loss}{Cost price}  × 100\)

• Discount = List Price - Selling Price

• Discount percentage =\( \frac{Discount}{List price}  × 100\)

• Slope of a line \((m) = \frac{y^2 - y^1}{x^2 - x^1}\), where (x1, y₁) and (x2, y2) are the joining two points 

• Point-Slope Form of a line: y - y₁ = m(x - x₁)

• Distance between two points (x₁, y₁) and (x₂, y₂): d = √(x₂ - x₁)² +(y₂ - y₁)² 

Pre-algebra introduces the fundamental concepts of algebra and helps students understand more complex algebraic topics. Here, we learn the difference between algebra and pre-algebra.

Mastering pre-algebra helps students build strong problem-solving skills, logical thinking, and confidence in handling real-world math situations. Here are some simple and effective tips for students to understand pre-algebra easily!

 

• Understand the basics first: Make sure you’re confident with whole numbers, fractions, and decimals before moving to pre-algebra topics. Strong basics make solving equations much easier.
  
   
• Learn the meaning of variables: Think of a variable (like x or y) as a 'mystery number' you need to find. This mindset makes equations and expressions feel like fun puzzles instead of confusing problems.
  
   
• Master the order of operations (BODMAS): Always remember BODMAS (Brackets, Orders, Division/Multiplication, Addition/Subtraction). Following this rule ensures your answers are always correct.
  
   
• Practice step-by-step solving: Always write down every step when solving problems. It helps you avoid small mistakes and clearly see how each number changes through the equation.
  
   
• Use games and online tools: Interactive math games, apps, and quizzes make pre-algebra practice fun. They help reinforce formulas, patterns, and number relationships in an engaging way.

Learning pre-algebra helps students to understand and work with variables, expressions, and equations in real-world situations. Now let’s learn how pre-algebra is used in everyday life. 

• Cooking and recipe adjustments: In Cooking, pre-algebra is used to adjust recipes by doubling, halving, or scaling them. For example, if making 20 cupcakes requires 2 cups of flour and 134 cups of sugar, pre-algebra helps determine how much of each ingredient is needed to make 10 or 30 cupcakes.

• Shopping and discounts: To calculate the discount while shopping, we use pre-algebra formulas: Discount = List Price - Selling Price, and Discount percentage = Discount/List price  × 100. It helps us to understand which store has the best deals. 

• Sports and game scores: In sports, to track scores and calculate the average scores, we use pre-algebra. It helps to analyze and track the performance of individuals.

• Budgeting: When planning trips, we use pre-algebra to estimate the distance, fuel use, and time. For example, if you get ₹500 as pocket money and spend ₹150 each week, you can use equations to find how many weeks your money will last.
  
  
   
• Mobile data and internet usage: Students often monitor data usage. Pre-algebra helps calculate how long a data plan will last. If you use 1.5 GB daily from a 30 GB plan, equation: 1.5𝑥 = 30 → 𝑥 = 20 days.