Types of Functions

A function is a mathematical rule where each input has only one output. In other words, every element of the domain is mapped to one element in the co-domain.

It is generally denoted as y = f(x), where x is the input and f(x) the output. In a function, the domain is the set of input values (x-values).

A domain can be the set of numbers, angles, decimals, or fractions, depending on the type of function. Range is the set of all possible output values (y-values) of the function.

To show the relationship between the domain and the range, we represent functions in three ways. Let’s now look at the three common representations.

Algebraic form: In an algebraic form, a function can be expressed as an equation like \(y = f(x)\), which shows how each input value x relates to the y-values.

Examples:

\(f(x) = x³\)

\(f(x) = sin (x)\)

These equations help us find the output for any given input.

Graphical form: A function can also be represented graphically using a coordinate plane. The graphical representation helps us to understand the function, that is if the function is increasing, decreasing, or constant. By plotting points on the graph, we can observe a pattern or trend in the function’s behavior.

Roster form: To represent a function as a collection of ordered pairs, we use the roster form. In this form, each element of the domain (x) is matched with exactly one corresponding element in the range(f(x)).

For example, if \(f(x) = 2x\), where x is a natural number ≤ 4, then the function can be represented as:

{(1, 2), (2, 4), (3, 6), (4, 8)}.

In each pair, the first element is from the domain and the second element is from the range.

In a function f: X → Y, the set X is called the domain, and it consists of all possible values. The set Y is the co-domain, and it includes all outputs of f. The range of the function refers to the actual output values (images) of elements from the domain, and is always a subset of the co-domain.

The given image illustrates the domain, co-domain, and range of the function. Note that only the elements in the co-domain that are actually mapped from the domain are included in the range.

For the given function:

• Domain = {a, b, c}
   
• Co-domain = {1, 2, 3, 4, 5}
   
• Range = {1, 2, 3}

Learning the different types of functions helps us analyze their properties more effectively. We classify the function \(y = f(x)\) into different types based on certain factors like their mapping, degree, and mathematical concepts.

The different types of functions are:

• Based on mapping
   
• Based on degree
   
• Based on mathematical concepts
   
• Miscellaneous functions

Based on mapping: As we have learned, a function is a rule that gives one output for each input. Functions can be classified based on how their elements map to the co-domain. The types of functions based on mapping are:

1. One-to-one function (injective):In this function, each input gives a different output.

Example:

\(f(x) = x + 1\)

i.e., if \(x = 1 → f(x) = 2\), and if \(x = 2 → f(x) = 3\)

In a one-to-one function, no two inputs have the same output.

2. Many-to-one function: In this type, multiple inputs can produce the same output.

Example:

\(f(x) = x²\)

If \(x = 2 → f(x) = 4\), and if \(x = −2 → f(x) = 4\)

i.e., two different inputs have the same output

3. Onto function (subjective): When every value in the co-domain is mapped with the domain, then it is said to be an onto function.

Example:

\(f(x) = 5 − x\) where x ∈ {1, 2, 3, 4, 5} and output set is {0, 1, 2, 3, 4}

(Each value in the output set is matched)

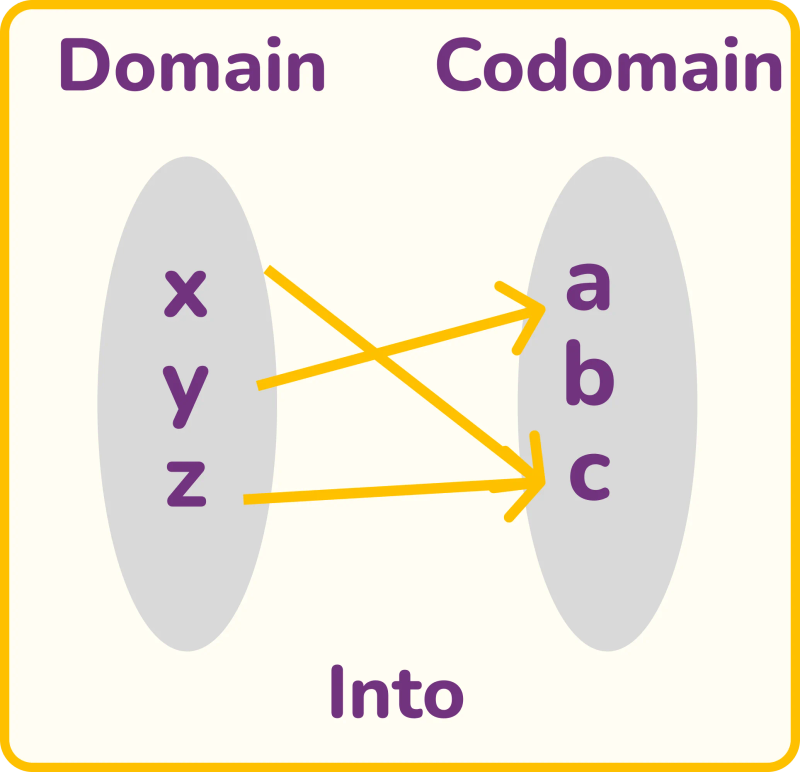
4. Into function: When some values in the output set are not utilized, it is said to be an into function.

Example:

\(f(x) = x²\), where x ∈ {1, 2, 3},

co-domain = {1, 2, 3, 4, 5, 6, 7, 8, 9}

Since f(x) only gives 1, 4, and 9, it’s an into function.

We classify functions based on their degree, that is, the highest exponent of the variable in the equation. Such functions are also called polynomial functions. Let’s look at its different types in detail:

• Constant function
   
• Linear function
   
• Quadratic function
   
• Cubic function

Identity function: The identity function is a function in which all elements in the domain are mapped to the range. It is written in the form \(f(x) = x\) or \(y = x\). When plotted on a graph, the identity function forms a straight line.

Constant function: A constant function is a function in which every element in the domain maps to the same value in the range.
 
Form: \(f(x) = K\) (K is a constant)

In this type of function, the output remains constant for all input values.

Example: \(f(x) = 5\) → Output is always 5.

Linear function: The type of polynomial function in which the highest power of the variable is 1 is known as a linear function.

Form: \(f(x) = mx + c\)

Here, m represents the slope and c represents the y-intercept 

Example: \(f(x) = 2x + 3, f(x) = x\)

The linear function is represented by a straight line graph (increasing, decreasing, or constant). A special case of a linear function is the identity function \(f(x) = x\), where output equals input.

Quadratic function: A quadratic function is a second-degree polynomial, where the highest degree of the variable is 2. The graph of a quadratic function is a parabola (U-shaped curve)

Form: \(f(x) = ax² + bx + c. where, (a ≠ 0)\)

Example: \(f(x) = x² - 4x + 3\)

Cubic function: In a cubic function, the highest power of x is three.

Form: \(f(x) = ax³ + bx² + cx + d.\ where, (a ≠ 0)\)

Example: \(f(x) = x³ - 2x² + x\)

The visual representation of this function on a graph gives a curve that may bend or change direction, often displaying a shape more complex than that of a quadratic function.

Polynomial function: A polynomial function can be represented in the form: 

\(f(x) = a_n x^n + a_{n-1} x^{\,n-1} + \dots + a_1 x + a_0 \)

Where, n represents a non-negative integer and x represents a variable.

Both the domain and range of a polynomial function are R.

Polynomial functions can be classified as quadratic, cubic, and so on, depending on the highest power (exponent) of the variable in the equation. The degree depends on the highest exponent of x.

Functions are widely utilized in various areas of mathematics. Depending on the concept they are used in, functions are further divided into different types. For example, the functions that are used in trigonometry are called trigonometric functions. The functions based on mathematical concepts are listed below:

Algebraic functions: Algebraic functions involve operations like addition, subtraction, multiplication, division, and powers of variables. They include constants, coefficients, and variables.

A general form of an algebraic function is:

\(f(x) = a_n x^n + a_{n-1} x^{\,n-1} + \dots + a_1 x + a_0 \)

Algebraic functions can be represented graphically and are further classified based on the degree of the polynomial:
 

• Linear functions
   
• Quadratic functions
   
• Cubic functions
   
• Polynomial functions
   

Trigonometric functions: Trigonometric functions relate angles to the ratios of sides in a right-angled triangle. They are based on the Pythagorean theorem. The six basic trigonometric functions are:
 

• \(f(θ) = sin θ\)
   
• \(f(θ) = cos θ\)
   
• \(f(θ) = tan θ\)
   
• \(f(θ) = sec θ\)
   
• \(f(θ) = cosec θ\)
   
• \(f(θ) = cot θ\)
   

The angle measured in degrees or radians is the θ

Inverse trigonometric functions: The functions that are the reverse of trigonometric functions are known as inverse trigonometric functions. They help to find angles when the trigonometric ratio is known.

The six inverse functions are:
 

• \(f(x) = sin⁻¹x\)
   
• \(f(x) = cos⁻¹x\)
   
• \(f(x) = tan⁻¹x\)
   
• \(f(x) = sec⁻¹x\)
   
• \(f(x) = cosec⁻¹x\)
   
• \(f(x) = cot⁻¹x\)
   

In these functions, the domain is a real number, and the range is an angle. Since their values repeat over intervals, they are known as periodic functions.

Logarithmic and exponential functions: The logarithmic function is the inverse of the exponential function.

The logarithmic function is generally denoted in the form:

\(y = logₐx\)

Where, a is the base, and it indicates the number of times the base must be raised to get x.

The corresponding exponential form is:

\(x = aʸ\)

These functions are widely used in higher-level mathematics and real-world applications such as compound interest, population growth, and scientific calculations.

In addition to these types of functions, there are several other important functions used across different mathematical contexts. These are described below:

Modulus function: The modulus function outputs the distance of a number from zero on the number line without considering its sign. It is denoted as:

\(f(x) = |x|\)

This means that whether x is positive or negative, the output is always non-negative. The graph of the modulus function appears in the first and second quadrants because the output \(y = |x|\) is always positive or zero. For example, points (x, y), there is a corresponding point (-x, y), making the graph symmetric with respect to the y-axis.

Rational function: A rational function is a fraction made up of two algebraic expressions, typically in the form:

\(f(x) = \frac {p(x)}{q(x)}\), where \(q(x) ≠ 0\)

A function is undefined at any point where its denominator equals zero. The graph of a rational function often includes asymptotes of horizontal or vertical lines that the graph approaches but never touches.

Signum function

The signum function (or sign function) indicates the sign of the input number. It doesn’t give a specific value but specifies whether it is positive, negative, or zero.

The range of this function is: {-1, 0, 1}

If \(x > 0 → f(x) = 1\)
If \(x = 0 → f(x) = 0\)
If \(x < 0 → f(x) = -1\)

This function is commonly used in programming and logic-based applications like conditional branching, sign detection in algorithms, and many more. 

Even and odd functions: These functions are categorized based on how they behave when the input is replaced by its negative:

A function is even if: \(f(-x) = f(x)\)

(The graph is symmetric about the y-axis)

Examples: \(f(x) = x², f(x) = cos (x)\)

A function is odd if: \(f(-x) = -f(x)\)

(The graph is symmetric about the origin)

Examples: \(f(x) = x³, f(x) = sin (x)\)

Periodic function: A function is called periodic if it repeats its values in regular intervals. In simple terms, for some value T, the function satisfies:

\(f(x + T) = f(x)\) for all x

Trigonometric functions like \(sin (x)\) and \(cos (x)\) are classic examples, repeating every 2π. For instance, \(f(x) = sin (x)\) has a period of 2π and a range of [-1, 1].

Inverse function: The inverse function of \(f(x)\), written as \(f⁻¹(x)\), essentially reverses the effect of \(f(x)\). In the inverse:

When the domain is \(f(x)\) then the range is \(f⁻¹(x)\)

The range of \(f(x)\) becomes the domain of \(f⁻¹(x)\)

An inverse function exists only if the original function is bijective (both one-to-one and onto).

Example:

If \(f(x) = x²\), then the inverse of \(f⁻¹(x) = √x\) (with domain restrictions).

For \(f(x) = sin x\), \(domain = ℝ\) and \(range = [-1, 1]\).

For \(f⁻¹(x) = sin⁻¹x\), \(domain = [-1, 1]\) and \(range = [-π/2, π/2]\).

Greatest integer function: Also known as the floor function, this function maps any real number to the greatest integer less than or equal to it. It is written as:

\(f(x) = ⌊x⌋\)

Example: \(⌊2.8⌋ = 2, ⌊-1.3⌋ = -2\)

The output is always an integer, and the graph appears as a step curve due to its jump at every integer value.

Domain: All real numbers (ℝ)

Range: Integers (ℤ)

Composite function: A composite function is formed by applying one function to the output of another. If f(x) and g(x) are two functions, then the composite function is:

\(f∘g(x) = f(g(x))\)

In this case, the output of g(x) becomes the input for f(x).

Example:

Let \(f(x) = 2x + 3\) and \(g(x) = x + 1\)

Then, \(f∘g(x) = f(g(x)) = f(x + 1) = 2(x + 1) + 3 = 2x + 5.\)

Graphs of different types of functions: Each type of function has a unique graphical representation and must satisfy the vertical line test to be considered a function. The shape of the graph varies based on the type of function.

For example:
 

• A linear function produces a straight line.
   
• The graph of a quadratic function is a U-shaped curve known as a parabola.
   
• A sine or cosine function has a wave-like pattern.
   
• Absolute value functions create a V-shaped graph.
   

The figure below shows the graphs of various other types of function types. Many of these graphs include horizontal, vertical, or even both types of asymptotes, depending on the nature of the function.

Here are some of the tips and tricks to master different types of functions for learners.
 

1. Use graphs to recognize functions. Learn the representations of each graph. If it is a straight line, it is a linear function. Similarly, quadratic, cubic absolute value are represented by U-shaped parabola, S-shaped curve, V-shaped graphs respectively.
    
2. Apply the vertical line test to check if a relation is a function or not. Draw vertical lines on the graph. If it touches the graph more than once, it is not a function. This is a great visual trick for beginners.
    

3. Practice it with graph matching. Draw or print graphs and match them with function equations. It helps in visual and analytical understanding together.
    

4. Connect the use of functions to real life. Kids learn faster when they see why it matters. Linear is used to calculate money earned per hour.  On the other hand, quadratic is used to calculate ball thrown height over a give period of time. While exponential is used to calculate population growth or viral spread.
    

5. Encourage your kids to practice function operations regularly. Start with numbers before moving to algebraic expressions.

Learning the different types of functions helps students solve real-life problems. Let’s now look at some real-life applications:

1. We can use a linear function to determine the total cost of a taxi ride, where you pay a fixed starting fare plus a set amount for every kilometer driven.
    
2. Exponential functions are used in the banking sector to calculate compound interest. Radioactive decay can also be calculated because the quantity decreases exponentially over time
    
3. Quadratic function is used to analyze the path a ball follows in sports or physics, as it forms the shape of a parabola.
    
4. Cubic functions can help us in calculating volume changes. The volume of a container depending on side lengths. Similarly, they can help us in calculating population growth models in some scenarios.
    
5. Absolute value functions can be used for distance measurements, difference in temperature, difference between actual and expected balance in banking.