Transformation Matrix

A square matrix used to represent the linear transformation in a vector space using matrix multiplication is called a transformation matrix.

It changes the coordinates of vectors while preserving their linearity and structure. By applying the rule of linear transformation, it changes the position vector of a point to a new vector. 

In linear transformation, the transformation matrix follows various properties. Here are some properties of transformation matrices:

 

 

• Transformation matrices are always square, which means they have an equal number of rows and columns. The order of a transformation matrix is the same as the dimensions of the vector space; for example, a \(2 × 2\) matrix operates in a 2D space.

 

• A composite transformation is obtained by multiplying the matrices of the individual linear transformations in sequence. 

 

• The transformation matrix that leaves the vectors unchanged is the identity matrix, and it is known as the identity transformation. 

 

• Transformation matrices can be combined using matrix multiplication, resulting in more complex transformation matrices. 
   

The transformation matrices can be classified into different types based on the specific transformation, such as:

 

 

• Translation Matrix

 

• Rotation Matrix

 

• Scaling Matrix

 

• Composite Matrix

 

• Reflection Matrix

 

• Shear Matrix

 

• Affine Transformation Matrix

 

 

Translation Matrix

 

The translation matrix is used to move the object along one or more axes (x, y, z), without changing the shape and orientation. Now let’s learn how it works, consider the point \(P = (x, y, z) \) in 3D space and apply the translation vector \(T = (Tx, TY, Tz) \).

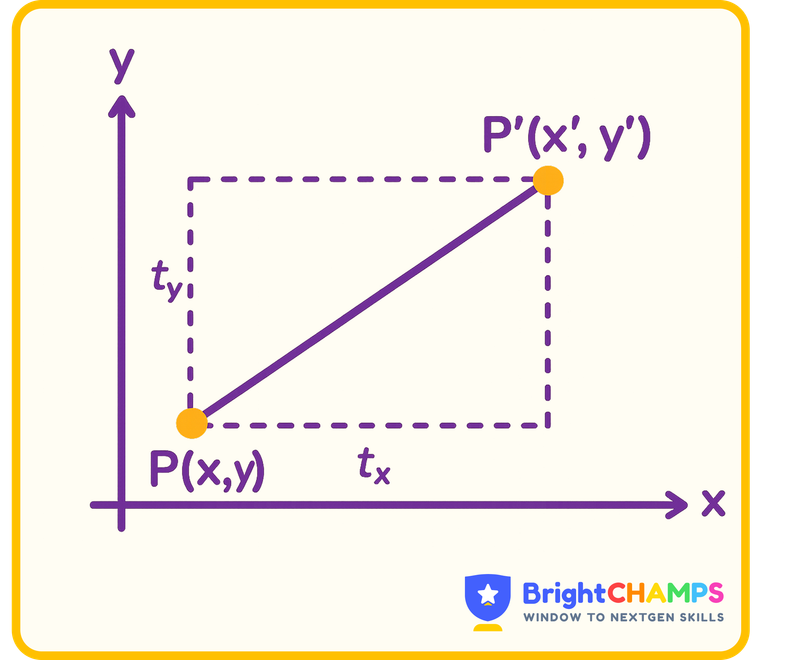
Here, the translation matrix is 
\(\begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \)

Representing the point P using a matrix: 
\(P = \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \)

Multiplying the transformation matrix by point p:

\(\begin{bmatrix} 1 & 0 & 0 & T_x \\ 0 & 1 & 0 & T_y \\ 0 & 0 & 1 & T_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} x + T_x \\ y + T_y \\ z + T_z \\ 1 \end{bmatrix} \)

Rotation Matrix

A rotation matrix is used to rotate vectors or points in a coordinate plane. In 2D, rotation is performed by a certain angle around a specific axis. In 3D, it occurs around a defined axis.  

 

For example, consider a point \(P = (x, y) \)in 2D. To rotate this point counterclockwise around the origin by an angle θ, we apply the 2D rotation matrix. 

 

Representing the point P(x, y) as: 
\(x = r cos ϕ \)
\(y = r sin ϕ\)

 

After rotation new coordinate (x′, y′) becomes:
\(x′ = r cos (ϕ + θ) = x cosθ - y sinθ \)
\(y′ = r sin (ϕ + θ) = x sinθ + y cosθ\)

It can be represented in matrix form as:

\([x′y′] = [cos⁡θ − sin⁡θ sin⁡θ cos⁡θ][xy]\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\)

 

 

Scaling Matrix

A scaling matrix is used to resize any object by expanding or contracting its vertices along the axes. Here, we multiply each coordinate of the vectors by the scaling factor. 
If the scaling factor is greater than 1, then the object expands, and if the scaling factor is less than 1, the object contracts. 

 

For example, the coordinates (X, Y) are scaled using the factors (SX, SY). Let’s consider the new coordinates (X′, Y′)
So, \(X' = X \cdot S_X \)
\(Y' = Y \cdot S_Y \)
It can be represented in matrix operations as: 

 

 

Composite Matrix

In a matrix, if we apply multiple transformations like scaling, translation, rotation, etc., in a sequence. Since matrix multiplication is non-commutative, the order of multiplication is important.

For example, translating the point \(P(1, 2) \) by \((3, 4)\) and then rotating it by 90° counterclockwise
The given point \(P = (1, 2)\)
\(T = (3, 4)\)
\(θ = 90°  \)

Writing the points in matrix form:

 

To apply translation, we multiply T and \(P (T \cdot P) \)

 

Thus, the translated point is \((4, 6)\)

Then, rotate the matrix 90° counterclockwise about the origin.
To find the rotation matrix, we use the formula, \(y'x' = (\sin\theta\cos\phi - \cos\theta\sin\phi) \, yx \)
So, \(R = \begin{bmatrix} \sin(90^\circ)\cos(90^\circ) & \cos(90^\circ) - \sin(90^\circ) \\ 1 & 0 - 1 \end{bmatrix} \)  

Here \((x, y) = (4, 6)\)
\(\begin{bmatrix} 1 & \Box \\ 0 & -1 \end{bmatrix} \begin{bmatrix} 6 \\ 4 \end{bmatrix} = \begin{bmatrix} 1 \cdot 4 + 0 \cdot 6 \\ 0 \cdot 4 + (-1) \cdot 6 \end{bmatrix} \)
\(=    4-6 \)

Thus, the point after rotation is (-6, 4)

 

 

Reflection Matrix

The transformation matrix is used to create mirror images of a shape. Here, the coordinates will be reversed, but the size and shape of the object remain the same.
For example, reflecting a point p(1, 2) across the x-axis
The reflection matrix across the x-axis can be represented as:

\(Rx = Rx = [100−1]R_x = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix} \)

Representing the point P(1, 2) in matrix
\(P = 21  \)
Now, to find the reflection matrix, we multiply Rx and P

\([100−1][12]=[1−2]\begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix} \begin{bmatrix}1 \\ 2\end{bmatrix} = \begin{bmatrix}1 \\ -2\end{bmatrix} \)

\(R_x \cdot P = \begin{bmatrix} 0 & 1 \\ -1 & 0 \\ 2 & 1 \end{bmatrix} \)
\(= \begin{bmatrix} 0 \cdot 1 + (-1) \cdot 2 & 1 \cdot 1 + 0 \cdot 2 \end{bmatrix} \)
\(= \begin{bmatrix} -2 & 1 \end{bmatrix} \)

So, after reflection, the point \(P(1, 2)\) becomes \(P′(1, -2) \)

 

 

Shear Matrix

A shear transformation is a type of transformation that slants the shape of an object along the coordinate axes. To skew objects in a coordinate system, we use a shear transformation, which is represented by a shear matrix. The shear transformation is classified into two types based on the axis of coordinates: X-Shear and Y-Shear. 

X-Shear(Xsh): The x-coordinates of the points are shifted while the y-coordinates remain unchanged. It can be represented as: 

\(X-Shear=[1kx01]\text{X-Shear} = \begin{bmatrix}1 & k_x \\ 0 & 1\end{bmatrix} \)

 

Affine Transformation Matrix

 

It is a type of geometric transformation that keeps the straightness and parallelism between lines. Commonly used in computer software and graphic design to move, scale, or rotate shapes.

 

We use homogeneous coordinates in affine transformation with matrices. So, let’s see how to express affine transformations using matrix multiplication.
Representing the vector (x, y) as a 3-vector (x, y, 1). Using matrix multiplication, we can represent all transformations. 

In matrix form, a translation that shifts a point by tx and ty  along the x-axis and y-axis, respectively, can be represented as:

\( [10tx01ty001]\begin{bmatrix}1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1\end{bmatrix} \)

Thus, \(x′ = x + tx \)
\(y′ = y + ty \)
 

Working with transformation matrices can be made easier by keeping a few things in mind.

• Understand each type – Know the difference between translation, rotation, scaling, and reflection matrices.

• Use homogeneous coordinates – Add the extra row/column for easier combination of transformations.

• Multiply carefully – Matrix multiplication is not commutative; order matters.

• Visualize the effect – Draw simple shapes to see how the transformation changes their position or orientation.

• Combine transformations – Use a single matrix to apply multiple transformations efficiently.

In mathematics, a transformation matrix is used to represent the linear transformation in a vector space. Here are some real-world applications of the transformation matrix.

 

• In computer graphics and animation, the transformation matrix is used to transform 2D and 3D models by rotating, scaling, translating, and shearing. 

 

• In image processing, the transformation matrix is used in medical imaging, facial recognition, and photo editing software. 

 

• In mathematics and physics, the transformation matrices are used in linear transformations, change of basis, coordinate transformations, and in quantum mechanics. 
   

• Robotics and engineering: Transformation matrices are used to control the movement and orientation of robot arms, drones, and mechanical systems in 2D and 3D space.
   

• Augmented Reality (AR) and Virtual Reality (VR): Transformation matrices help position, rotate, and scale virtual objects accurately within real-world or simulated environments.