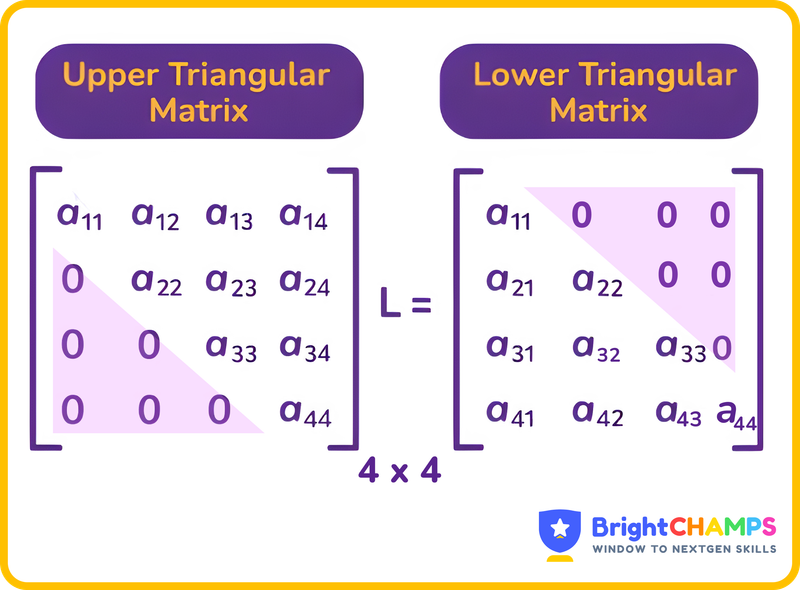
Triangular Matrix

A triangular matrix is a specific form of a square matrix. It is obtained when all the elements either above or below the principal diagonal are zero. Triangular matrices are classified into two types: upper triangular and lower triangular. An upper triangular matrix is a square matrix where all the entries below the main diagonal are zero, while in a lower triangular matrix, all the entries above the main diagonal are zero. 

Triangular matrices have several useful properties when computing determinants. For example:

 

• First, a triangular matrix is invertible if none of its diagonal elements are zero. 
   

• Second, since the characteristic polynomial of a triangular matrix is determined by its diagonal elements, finding eigenvalues and eigenvectors becomes straightforward. 
   

• Third, if a triangular matrix is positive semidefinite, then its inverse, when it exists, is also positive semidefinite.

In a linear transformation, changes in one variable lead to proportional changes in others. The determinant of a matrix represents how much a linear transformation scales space. The determinant of a triangular matrix is calculated by multiplying all the entries on its main diagonal. Let’s take an example to understand how to compute the determinant:

Upper triangular Matrix:

\( A = \begin{bmatrix} 2 & 3 & 4 \\ 0 & 5 & 6 \\ 0 & 0 & 7 \end{bmatrix} \)
                                

• Diagonal elements: 2, 5, 7
   
• Determinant: det(A) = 2 × 5 × 7 = 70

Lower Triangular Matrix:

\( B = \begin{bmatrix} 1 & 0 & 0 \\ 4 & 3 & 0 \\ 7 & 5 & 6 \end{bmatrix} \)
 

• Diagonal elements: 1, 3, 6
   
• Determinant: det(B)=1 × 3 × 6 = 18
   

In triangular matrices, the determinant remains unchanged by the zeros located outside the main diagonal.

LU Decomposition and Triangular Matrices

LU decomposition (also called factorization) of a square matrix 𝐴 expresses A = LU, where L is lower-triangular with 1s on the diagonal (or unit lower triangular) and U is upper-triangular.

The connection is that solving 𝐴𝑥 = 𝑏 becomes LUx=b, and Ly = b can be solved by forward substitution, then 𝑈𝑥 = 𝑦 by backward substitution. 

For example, we have: \( A = \begin{bmatrix} 4 & 3 \\ 6 & 3 \end{bmatrix} \)

We want to find L and U such that A = LU. 
 

Step 1: Let, \( L = \begin{bmatrix} 1 & 0 \\ l_{21} & 1 \end{bmatrix} \)

                    \( U = \begin{bmatrix} u_{11} & u_{12} \\ 0 & u_{22} \end{bmatrix} \) 
 

Step 2: Multiply 𝐿 and 𝑈. 
 

\( LU = \begin{bmatrix} 1 & 0 \\ l_{21} & 1 \end{bmatrix} \begin{bmatrix} u_{11} & u_{12} \\ 0 & u_{22} \end{bmatrix} = \begin{bmatrix} u_{11} & u_{12} \\ l_{21}u_{11} & l_{21}u_{12} + u_{22} \end{bmatrix} \)
 

Step 3: Compare with A. 

\( \begin{bmatrix} u_{11} & u_{12} \\ l_{21}u_{11} & l_{21}u_{12} + u_{22} \end{bmatrix} = \begin{bmatrix} 4 & 3 \\ 6 & 3 \end{bmatrix} \)

So, u₁₁ = 4, u₁₂ = 3, l₂₁u₁₁ = 6, l₂₁u₁₂ + u₂₂ = 3

From l₂₁u₁₁= 6, we get l₂₁ = \(\frac{6}{4}\) = -1.5
 

Therefor \( L = \begin{bmatrix} 1 & 0 \\ 1.5 & 1 \end{bmatrix} \) 
 

               \( U = \begin{bmatrix} 4 & 3 \\ 0 & -1.5 \end{bmatrix} \) 
 

and \(A = LU\)

Triangular matrices are of two main types, each defined by the position of their zero elements relative to the main diagonal.

1. Upper triangular matrix: The upper triangular matrix is a square matrix where all the entries below the main diagonal are zero, while the elements on and above the diagonal can be non-zero.

Example: \( \begin{bmatrix} 2 & 3 & 1 \\ 0 & 5 & 4 \\ 0 & 0 & 7 \end{bmatrix} \)

2. Lower triangular matrix:  A lower triangular matrix is a square matrix where all elements above the main diagonal are zero, and the entries on and below the diagonal may be non-zero.

Example: \( \begin{bmatrix} 4 & 0 & 0 \\ 1 & 3 & 0 \\ 2 & 6 & 5 \end{bmatrix} \)

3. Strictly triangular matrix:  When the principal diagonal has all zero elements, the matrix is strictly triangular.
Strictly upper triangular matrix: This type of matrix has zeros on the main diagonal and everywhere beneath it. Only the values above the diagonal can be non-zero.

Strictly lower triangular matrix: In this matrix, all the elements on the diagonal and above it are zero, while the entries below the diagonal can contain non-zero values.

4. Unit triangular matrix: A unit triangular matrix is a triangular matrix where every element along the main diagonal is equal to 1.
 

\( \begin{bmatrix} 1 & 0 & 0 \\ 2 & 1 & 0 \\ 4 & 3 & 1 \end{bmatrix} \)
 

A unit lower triangular matrix has all entries above the main diagonal as zero, and the diagonal itself is filled with 1s.

A unit upper triangular matrix has zeros below the main diagonal, with all diagonal elements being 1.
 

\( \begin{bmatrix} 1 & 5 & 3 \\ 0 & 1 & 2 \\ 0 & 0 & 1 \end{bmatrix} \)

5. Diagonal matrix: A diagonal matrix is a specific type of both upper and lower triangular matrices, where all elements outside the main diagonal are zero, and only the diagonal entries can be non-zero.

Example: \( \begin{bmatrix} 9 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 2 \end{bmatrix} \)

Triangular matrices are a foundational concept in algebra and linear algebra. Understanding their structure, properties, and patterns can make complex problems much easier. Here are some practical tips and tricks to help you master triangular matrices efficiently.

• Visualize the zeros: Always pay attention to the zeros above or below the main diagonal. Shading or highlighting the zero region in your notebook helps you quickly identify whether a matrix is upper or lower triangular.
  
   
• Remember determinant shortcut: The determinant of a triangular matrix is simply the product of its diagonal entries: 
  
  \( \det(T) = \prod_{i=1}^{n} T_{ii} \).
  
  
   
• Check invertibility quickly: A triangular matrix is invertible if all its diagonal entries are non-zero. This quick check helps you avoid unnecessary calculations.
  
   
• Use substitution methods efficiently: For lower triangular matrices, use forward substitution; for upper triangular, use backward substitution. Practice these methods step-by-step to solve systems of equations faster.
  
   
• Practice LU decomposition connections: Understand that any square matrix can often be decomposed into L × U, where L is lower triangular and U is upper triangular. Try small numeric examples to see how triangular matrices simplify computations.

Triangular matrices are useful in solving real-life problems in engineering, computing, and data analysis by making calculations simpler.

• Solving systems of linear equations: Many numerical methods (like LU decomposition) reduce complex systems to triangular matrices for fast computation using forward/backward substitution. Thus, triangular matrices are useful in fields like structural engineering (e.g., bridges, buildings) or circuit analysis.

• Computer graphics & 3D transformations: Triangular matrices are used in matrix factorizations (like QR) that help with transforming shapes, rotating them, and projecting 3D to 2D, and are used for rendering 3D objects in games, movies, or VR.

• Signal processing & filtering: Algorithms like Kalman filters (used in tracking systems or GPS) use triangular matrices for faster recursive calculations. Such algorithms are used in mobile communication, audio processing, or radar systems.

• Finance and risk modeling: Cholesky decomposition (which gives a lower triangular matrix) is used for efficiently simulating correlated variables in Monte Carlo simulations, used in portfolio risk analysis or option pricing models.

• Machine learning & data science: Algorithms like linear regression (with QR or LU decomposition), Principal Component Analysis (PCA), and neural network backpropagation benefit from triangular matrix simplification to speed up training and computation.