
4252 Learners
Numbers
Do you like counting your candies, checking the time on a clock, or telling everyone how old you are? It’s all because of numbers. Numbers help us count, measure, and describe things around us.
Share Post:
Trustpilot | Rated 4.7
1,292 reviews

What are Numbers in Math?

We use numbers every day in our lives, and they are often called numerals. Without numbers, we wouldn't be able to count things, check the date or time, or handle money. Numbers are used for many purposes, sometimes for measuring, sometimes for labelling, and often for calculations.
The properties of numbers allow us to perform various arithmetic operations, such as addition, subtraction, multiplication, and division. Numbers can be written both in figures and in words. For example, 2 is written as two, and 25 is written as twenty-five. For measuring height, weight, or temperature whether in sports, scores, and timings or for writing phone numbers, house addresses, and bus numbers, we use numbers to make our world easier.

Count real objects like fruits or toys to learn easily. Try counting in groups of 5s or 10s to spot patterns. Notice how numbers are formed, like “twenty-one” from “twenty” and “one.” For quick math, round numbers, for example, 49 + 77, where 50 + 77 – 1 = 126. To find how many numbers are between two values, use last - first + 1. For example, 12 – 8 + 1 = 5.
The number “zero (0)” plays a vital role in mathematics. It is used as a placeholder in the place-value system and serves as the additive identity in the real numbers. Zero represents nothing or the absence of quantity. For example, if there are three apples and now none are left, we use zero to show that.
In math, there are different types of numbers like:

History of Numbers
Numbers have not always looked the way they do today. Long ago, early humans used simple marks and symbols to keep count of things around them. As time passed, people created new ways to count and calculate more easily.
- Early humans used symbols and tally marks (////) to count things, but it was hard for large numbers.
- As civilization grew, people created different symbols to represent bigger quantities. Romans used I, V, X, L, C, D, M but had no zero.
- This system used only ten digits (0-9) to show any number. Aryabhata explained the concept of zero and place value. For example, even Pythagoras once said, "Everything in this world is made of numbers, even music".
- Arab merchants and scholars spread it to Europe, and today we call it the Hindu-Arabic numeral system, which is still used everywhere.
- Scientists believe counting systems first emerged in ancient societies like Egypt, Mesopotamia, and India.
- Different numeral systems were developed across the world, and as people traveled, these systems spread across continents. The Indian numeral system spread to the Middle East and Europe, becoming the base of the modern decimal system.
- The Brahmi script (around 3rd century BCE, during Emperor Ashoka's time) is the earliest known numeral system of India.
Brahmi numerals had symbols for 1-9 and special symbols for 10, 100, and 1000. They are considered the ancestors of modern numerals (0-9) used worldwide.
- Later, numbers were written in Devanagari script, which is used for Sanskrit.


Properties of Numbers
Numbers follow specific special rules are called properties that help us solve problems easily and understand math better. These properties demonstrate how numbers behave when we add, multiply, or combine them in various ways.
- Commutative Property
- Associative Property
- Distributive Property
- Identity Property
- Inverse Property
- Closure Property

Explore Our Programs



Types of Numbers
Numbers can be classified in different ways based on how we use them and their unique features. Let's explore the different kinds of numbers.
1. Natural Numbers - These are the basic counting numbers that start from 1 and go on without end. They are represented by the letter 'N'. For example: N = {1, 2, 3, 4, 5,...}
2. Whole Numbers - Whole numbers include all natural numbers along with 0. They are represented by the letter 'W'. For example, W = {0, 1, 2, 3, 4, 5,...}
3. Integers - Any positive, negative, or zero whole numbers are called integers. For example: -2, -1, 0, 1, 2,...
4. Rational Numbers - If a number is written as p/q, it is called a rational number, where q is not zero and both p and q are integers. For example: 1/2, -3, 57/100.
5. Irrational Numbers - These numbers can never be expressed as fractions. For example: π, √2.
6. Real Numbers - Rational and irrational numbers together make real numbers. For example, 2, -5, √3, 0.5.
7. Complex Numbers - Complex numbers consist of a real part and an imaginary part and are written in the form a + bi, where i = √(-1).


Special Types of Numbers
Numbers can be grouped based on their special types and usage. Let us see what are all the types of numbers.
Cardinal numbers: Cardinal numbers state how many of something are in a list, like 1, 5, 10, etc.
Ordinal numbers: Ordinal numbers define the position of something in a list, like 1st, 2nd, 3rd, 4th, and so on.
Nominal numbers: Nominal numbers are used as names. It does not denote an actual value or the position of something.
Pi: It is a special number approximately equal to 3.114159. Pi (π) is defined as the ratio of the circumference of the circle to the diameter of the circle.
Euler’s number: Another important irrational number is approximately 2.718. It is used in advanced math, such as logarithms and exponential growth.
Golden ratio: The golden ratio is a special number, approximately equal to 1.618. It is an irrational number, and its digits do not follow any pattern.

Number System
A number system is a method of representing numbers using digits, symbols, or specific rules. Each system is defined by its base and the number of unique digits it uses. A common example is the decimal system, which has a base of 10.
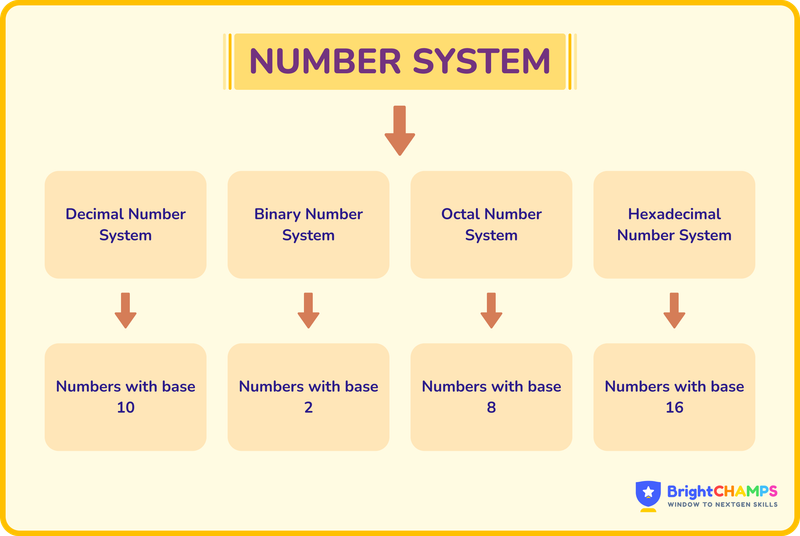
- Every number system uses a specific set of symbols and a base that shows how many unique symbols it includes.
- The decimal system has a base of 10 (digits 0-9).
- The binary system has a base of 2 (digits 0 and 1).
- In a positional system, the value of a digit depends on its position (like in the decimal system).
- In a non-positional system, each symbol has a fixed value no matter where it appears (like in Roman numerals).
The main purpose of a number system is to provide a clear, consistent way to write numbers for counting, measuring, and performing calculations.

How to Write Numbers in Words
Learn to convert numbers into words easily by breaking them into groups and writing each part with its period name, like thousands or millions.
- Break the number into periods - Group the digits in sets of three using commas. For example, 37,519,248 has three periods: millions, thousands, and ones.
- Write each period’s number - Start from the left and write the value in each period, followed by its name, like millions or thousands.
- Skip the “ones” label - The last group of digits doesn’t need a period name.
- Use commas correctly - Place commas between the word groups just as they appear in the number. For example,37,519,248 is written as thirty-seven million, five hundred nineteen thousand, two hundred forty-eight.
Here is a list of numbers from 1 to 50 in words to help you write numbers in order.


PEMDAS
The term PEMDAS stands for
- P – Parentheses,
- E – Exponents (powers and roots),
- M – Multiplication,
- D – Division,
- A – Addition,
- S – Subtraction.
PEMDAS represents the order of performing mathematical operations.
This can be understood better by using an example.
Solve :
\(8 + \left( \frac{6}{3} \right) \times 2^{2} \)
Step 1: Parentheses → \(6 \div 3 = 2 \)
Step 2: Exponents → \(2^{2} = 4 \)
Step 3: Multiplication → \(2 \times 4 = 8 \)
Step 4: Addition → \(8 + 8 = 16 \)
In this example, the correct order of operations that are performed is shown.


Importance of Numbers for Students
Numbers are significant for students because they play a crucial role in our daily lives. A good understanding of numbers makes learning math easier and more useful in daily life.
- A number is one of the building blocks of mathematics. Understanding numbers and how they relate to each other helps children learn more advanced math concepts later.
- Learning numbers helps children think better. It teaches them to follow sequences and solve problems, which improves their thinking capacity and helps them make connections.
- Learning numbers is also part of language development. When children learn numbers, they practice saying them. This helps improve their vocabulary and makes them better communicators.
- Knowing numbers well helps children do better in school. Children who grasp numbers early can learn not only math, but also other subjects more easily.
- Numbers play a crucial role in learning about money. Being good with numbers helps people understand and manage their finances, such as budgeting, saving, and making informed investments.
- Counting helps children understand that numbers represent real objects when they link numbers to the things around them.
- Children need to understand that numbers represent quantities and can be used to compare different amounts.
Begin your journey into Numbers by exploring key concepts. Understand important number topics in detail by selecting from the list below:

Tips and Tricks to Learn Numbers
Understanding numbers can be made simpler using a few tricks. Like a game, the more we practice, the easier it gets. Here are a few tips and tricks that can make understanding numbers easier.
- Practice number patterns - try skipping-counting (2, 4, 6…) or counting backward to strengthen your skills.
- Play math games - By using puzzles, flashcards, or online math games to make learning fun.
- Use visual aids - Drawing number lines, charts, or tables to understand number relationships.
- Teach through stories - Using simple stories that involve numbers, like counting apples or friends.
- Incorporate activities - Use games, songs, and hands-on tools like blocks or beads.
- Encourage group learning - Let students count or solve simple number problems together.
- Use real-life examples - Talk about numbers while shopping, cooking, or reading clocks.
- Limit pressure - Parents can make number learning fun and stress-free by using games, everyday examples, and gentle encouragement so their child feels confident and enjoys teaching numbers.

Common Mistakes and How to Avoid Them in Numbers
When learning about numbers, children may get confused since there are many topics to understand. Given below are a few mistakes that children make and how to avoid them.

Real-World Applications of Numbers
Numbers are an important part of our daily lives. They are used for simple and complex tasks. Here are a few real-world applications of numbers:
1. Budgeting and Accounting:

1. Budgeting and Accounting:
Ever wondered how you manage your pocket money, plan a trip, or save up for something you want to buy? That's numbers at work, balancing income, and other goals we want to reach.
2. Precision in the Kitchen:

2. Precision in the Kitchen:
While cooking or baking, the right measurement/quantity of ingredients is very crucial.
3. Mastering the Clock:

3. Mastering the Clock:
Time management in scheduling appointments, catching buses, or setting alarms.
4. Technology and Computing:

4. Technology and Computing:
In algorithms, computers use binary numbers, zeros, and ones.
5. Sports:

5. Sports:
Used in sports for calculating timing and statistics.
6. Medicine:

6. Medicine:
Medicine dosage calculations, MRI scans, X-rays, and similar medical procedures rely on accurate numbers to ensure patient safety and correct results.

Examples of Numbers

Problem 1
Find the missing two numbers if the sum of 2 consecutive natural numbers is 37.

Let the two consecutive natural numbers be x and x + 1.
\(x + (x+1) = 37\)
\(2x + 1 = 37\)
\(2x = 36\)
\(x = 18\)
\(Therefore, x + 1 = 19\)
Explanation
The two consecutive natural numbers are 18 and 19. The sum of 18 and 19 is 37.

Problem 2
Check whether 15 and 28 are co-prime.

To check if 15 and 28 are co-prime
The prime factors of \(15 = 3 × 5\)
The prime factors of \(28 = 2 × 2 × 7\)
Since there are no common factors other than 1, 15 and 28 are co-prime.
Explanation
Co-prime numbers have only 1 common factor between them, that is 1. Here, 15 and 28 have only 1 in common. Therefore, they are co-prime numbers.

Problem 3
Find the quotient of 8/3 ÷ 2/3.

To divide, \( \frac{8}{3} \div \frac{2}{3} \)
Multiplying\( \frac{8}{3} \) with the reciprocal of \( \frac{2}{3} \)
That is, \( \frac{8}{3} \times \frac{3}{2} = \frac{24}{6} \)
Simplifying the fraction, \( \frac{24}{6} = 4 \)
Explanation
To divide a fraction, we multiply the first fraction with the reciprocal of the second fraction. When we divide the given fractions, we get the quotient as 4.

Problem 4
Show that 5 + 7 is the same as 7 + 5.

Add in the given order, \(5 + 7 = 12.\)
Swap the order, \(7 + 5 = 12.\)
Explanation
The commutative property of addition says the order doesn’t matter. So, \(5 + 7\) and \(7 + 5\) both give the same result: 12.

Problem 5
Simplify (2 × 3) × 4 and 2 × (3 × 4).

First group: \((2 × 3) = 6 → 6 × 4 = 24.\)
Second group: \((3 × 4) = 12 → 2 × 12 = 24.\)
Explanation
The associative property says grouping doesn’t change the result in multiplication. So both methods give the same answer: 24.


FAQs on Numbers
1.Define natural numbers.
2.What are odd numbers?
3.What does Z mean in math?
4.What is a rational number?
5.What are prime numbers?
6.What are the types of numbers?
7.What are the properties of a number?
8.What is the difference between a number and an integer?
9.What is a number system?
10.What is the smallest number?
11.What is the absolute value of a number?
12.What is the Fundamental Theorem of Arithmetic?
13.Why is it important for my child to learn about numbers early?
14.How can parents make number learning fun for their child?
15.How can parents explain odd and even numbers to their child?


Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.

















