Factors of 144

The factors of 144 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72 and 144

 

Negative Factors: These are the negative counterparts of each positive factor.

Negative factors: -1, -2, -3, -4, -6, -8, -9, -12, -16, -18, -24, -36, -48, -72, -144

 

Prime Factors: Prime factors are the prime numbers themselves.

Prime factors: 2, 3

 

Prime Factorization: Prime factorization expresses the product of prime factors in its exponential form.

It is expressed as 2⁴ × 3²

 

Table listing the factors of 144
 

It is easy to find the factors of a number. We can identify the factors of 144 with the help of the methods mentioned below:

 

• Multiplication Method

 

• Division Method

 

• Prime Factor and Prime Factorization

 

• Factor Tree
   

The multiplication method finds the pair of numbers that when multiplied gives 144 as their product.

 

Step 1: Find all the numbers whose product is 144. 

Step 2: These numbers are the factors of 144

Step 3:Group these numbers as pairs.

 

Here’s a list of paired numbers whose product is 144:

 

1 × 144 =144

2 × 72 = 144

3 × 48 = 144

4 × 36 = 144

6 × 24 = 144

8 × 18 = 144

9 × 16 = 144

12 × 12 = 144

For the division method, the process of division will go on until the remainder becomes zero.

Step 1: 1 will always be a factor of any number because we can divide any number by 1.  Example: 144÷1 = 144. 

Step 2: Move to the next integer and continue this process until you can’t divide 144 anymore.

 

Overview of Factors of 144 using the division method

 

Prime factors are the prime numbers, having 1 and the numbers themselves as factors. Prime factorization is breaking down the number into its prime factors and expressing their product in exponential form.

Prime factors of 144: 2, 3

 

To find the prime factors of 144

Step 1: Divide 144 with the prime number 2

144÷2 = 72

72÷2 = 36

36÷2= 18

18÷2=9

Step 2: Divide 9 with the prime number 3

9÷3 = 3

3÷3 = 1

Prime Factorization of 144

For the prime factorization method, the product of prime factors of 144 is expressed as 2⁴ × 3²

The prime factorization is visually represented using the factor tree. In this factor tree, each branch splits into prime factors.

 

Factor Tree for 144:

 

 

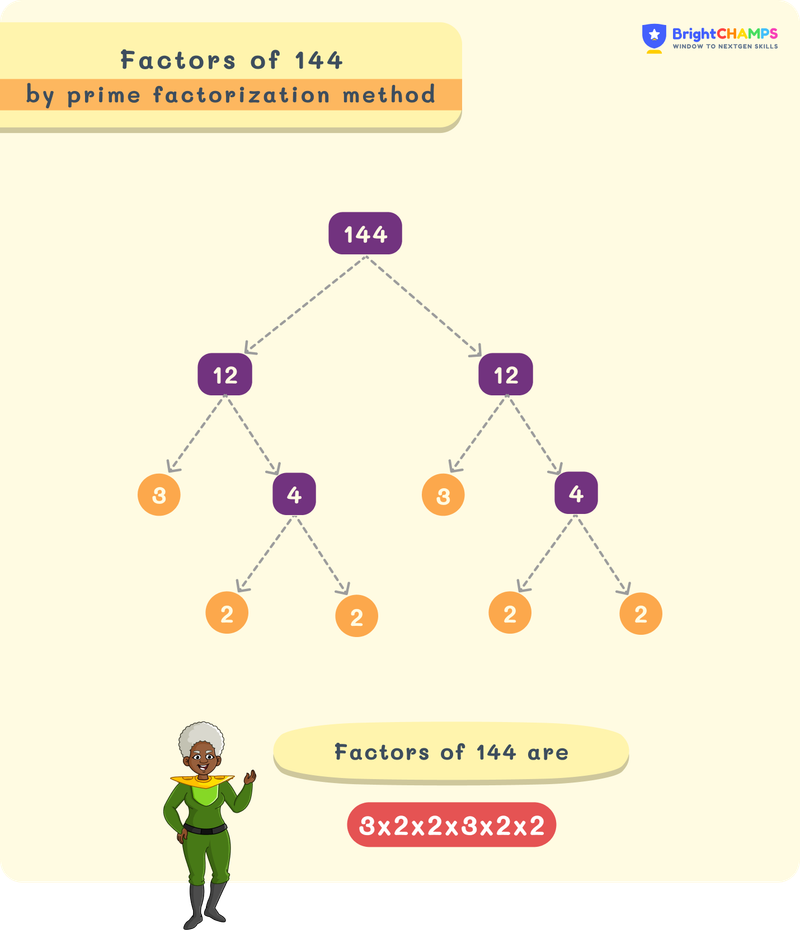
Factors of 144 can be written in both positive pairs and negative pairs. They are like team members. Their product will be equal to the number given.

 
Positive Factor Pairs: (1,144), (2,72), (3,48), (4, 36), (6,24), (8, 18), (9,16), (12,12)

 

Negative Factor Pairs:  (-1,-144), (-2,-72), (-3,-48), (-4, -36), (-6, -24),  (-8, -18), (-9, -16), (-12, -12)

• Divisor:  Number that divides another number

 

• Quotient: The number you get when you divide a number with another.

 

• Multiple: A number and any integer multiplied. 

 

• Prime Factor: A prime number having 1 and the number itself as its factor

 

• Prime Factorization: Process of breaking down the prime factors.