Factors Of 256

We can tell if a number has more than 2 factors just by seeing if a number is a prime number or not. As none of the even numbers except 2 are prime numbers, we can tell that 256 has more than 2 factors. Let us find what the factors are.

Negative factors of 256:  -1, -2, -4, -8, -16, -32, -64, -128 and -256.

Prime factors of 256: The prime factors of 256 is 2.

Prime factorization of 256: 2×2×2×2×2×2×2×2

The sum of factors of 256: 1+2+4+8+16+32+64+128+256= 511.
 

Children use multiple ways to find factors of a number. Let us look at some ways we can use to find the factors of 256.

 

• Multiplication Method

 

• Division Method

 

• Prime Factor and Prime Factorization
   

In the multiplication method, we find pairs of numbers where the product will be 256. In this process, possible steps will be - 

Step 1: Find all those numbers whose product will be 256.

Step 2: These numbers will be called the factors of 256.

Step 3: Students have to write these pairs of numbers for this method.

List of numbers whose product is 256

256×1= 256

128×2= 256

64×4= 256

32×8= 256

16×16= 256

So the pair of numbers whose product is 256 are (1,256), (2,128), (4,64), (8,32), and (16,16).
 

For the division method, the process of division will go on until the remainder becomes zero.

Step 1: For the division method, always try the smallest number to start with. It is advisable to start dividing the number by 1, then both the number and 1 will be its factors. Example: 256÷1 = 256.

Step 2: Then check with the next number to see whether the number is divided completely without any remainder. Both divisor and quotient are the factors. Example: 256÷2= 128 and so on.
 

Prime Factors Of 256: The prime factors of 256 is 2. We find the prime factors of 256 by two ways.

 

 Prime Factorization: Here we will divide the numbers by the smallest prime number. Till we completely divide the given number. For 256, the steps are like this:

256/2= 128

128/2= 64

64/2= 32

32/2= 16

16/2= 8

8/2= 4

4/2= 2

2/2= 1

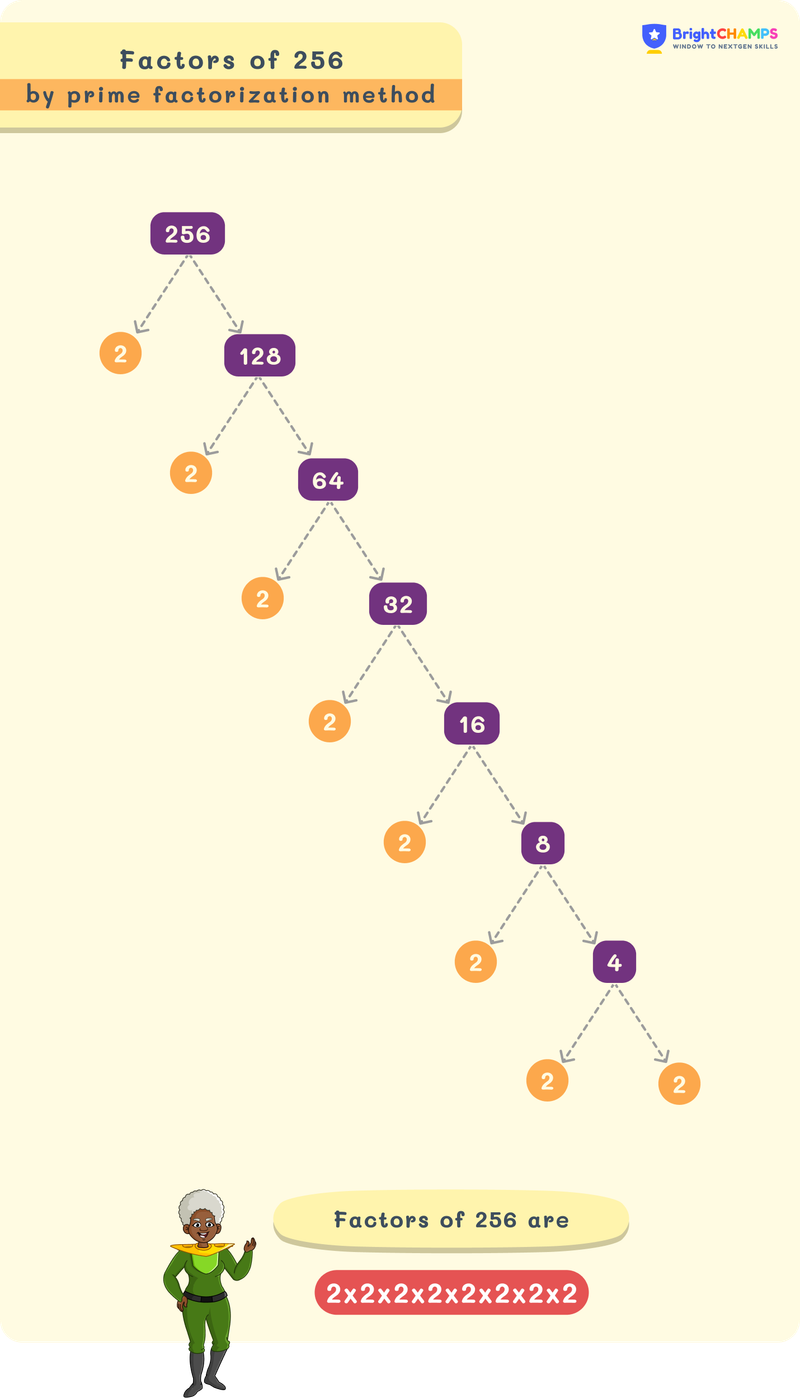
As 2 is a prime number, it is only divisible by 2. Hence, The prime factorization of the number 256 is 2⁸.
 

This is a very easy method because in many ways it’s almost the same as a prime factorization. We will break down huge numbers in this case to get what we call a factor tree.

Step 1: 256 divided by 2 gives us the answer being 128.

Step 2: 128 divided by 2 gives us 64.

Step 3: 64 divided by 2 gives us 32.

Step 4: 32 divided by 2 gives us 16.

Step 5: 16 divided by 2 gives us 8.

Step 6: 8 divided by 2 gives us 4.

Step 7: 4 divided by 2 gives us 2.

Step 8: 2 divided by 2 gives us 1.

Step 9: This can’t be divided further.
 

There are positive and negative factor pairs for a given number. Let us look at these factor pairs.

Positive Factor Pairs: (1,256), (2,128), (4,64), (8,32)  and (16,16).

Negative Factor Pairs: (-1,-256), (-2,-128), (-4,-64), (-8,-32)  and (-16,-16).
 

• Factors: Factors are numbers that can be multiplied together to yield a specific product, leaving no remainder when dividing the original number evenly.

 

• Prime Numbers: Prime numbers are natural numbers greater than one that have no positive divisors other than 1 and themselves, meaning they cannot be divided evenly.

 

• Remainder: A remainder is the amount left over after division when one number cannot be divided evenly by another, indicating incomplete division.

 

• Multiplication Method: The multiplication method involves identifying pairs of numbers that multiply together to produce a given number, illustrating how factors relate to multiplication.