Summarize this article:
 365 Learners
365 LearnersLast updated on December 10, 2025
Multiplication on Number Line

Multiplication on a number line is a visual way to represent and understand multiplication as repeated addition. The number line is a straight line where numbers are placed at equal intervals. Number lines are used to perform the basic operations such as addition, subtraction, division, and multiplication.

What is Multiplication on a Number Line?

Multiplication on a number line is a visual method of representing repeated addition by making equal jumps along the line. The horizontal line with equal intervals on an infinite line, that extends on the both sides. The numbers keep on increasing as we move from left to right. In order to perform multiplication on a number line, let us start from zero and move towards the right side for a given number of times.
Example 1: 4 × 3
To multiply 4 × 3 on a number line, we show it as 3 equal jumps of 4.
Steps:
Begin at 0.
Make 3 jumps, and each jump moves 4 units to the right.
You land on the numbers: 0 → 4 → 8 → 12.
Final Answer:
\(4 × 3 = 12\)

How to Do Multiplication on a Number Line?
Follow these steps to perform multiplication on a number line:
Step 1: Draw a number line
First, draw a straight line. Then, place points evenly on the line to represent the numbers. The middle of the line shows the starting point zero, and from the right-hand side of zero, all the positive numbers are placed and on the left-hand side of zero all the negative numbers are placed.
Step 2: Identify how to jump places:
For example, when multiplying 5 × 2, we must understand that 5 represents how many times we have to make a jump. While on the other hand, 2 represents the interval of the group that needs to be followed.
Step 3: Start at zero (0)
Always begin at 0 on the number line. This ensures accurate counting of jumps.
Step 4: Make equal jumps:
Move right for positive multipliers and left for negative multipliers. Move left if we are multiplying by a negative number. Each jump should be equal.
Step 5: Mark the final position:
The number where you land after the last jump is the product (answer). Circle or highlight this final position for clarity.

We follow the same steps for cases like negative multiplications and fractional multiplications.
Multiplication of fractions on number line:
While dealing with fractional multiplications like \(3 \times \frac{1}{2} \), we make jumps of the fractional amount. Starting from 0, we must make 3 jumps of size \(\frac{1}{2} \). The final jump will land on \(1 \tfrac{1}{2} \).

Multiplication of a negative number on number line:
When we are dealing with a negative number like \(4 × (- 2)\), we have to make 2 jumps of size 4 on the left side from zero. The final jump will land on - 8.

Properties of Multiplication on Number Line
Various properties are applicable for multiplication, such as associative, distributive, identity, commutative, and so on. The properties of multiplication on number line are mentioned below in detail:
- Associative property:
Rule: \((a × b) × c = a × (b × c)\)
Multiplication is associative, meaning the way numbers are grouped does not change the result.
For example,
Solve:
\((2 × 3) × 4\)
First, find
\(2 × 3 = 6\)
Then,
\(6 × 4 = 24 \)
Solve:
\(2 × (3 × 4)\)
First, find
\(3 × 4 = 12\)
Then,
\(2 × 12 = 24\)
Since both results are 24, the property holds
- Distributive property:
Rule: \(a × (b + c) = (a × b) + (a × c)\)
In multiplication, the operation distributes over addition.
Example on a Number Line:
Solve: \(2 × (3 + 4)\)
\(3 + 4 = 7\), so
\(2 × 7 = 14\)
Solve: \((2 × 3) + (2 × 4)\)
\(2 × 3 = 6\),
\(2 × 4 = 8\), so
\(6 + 8 = 14\)
Both ways lead to 14, proving the property.
- Identity property:
Rule: \(a × 1 = a\)
Any number multiplied by 1 remains the same.
Example on a Number Line:
\(5 × 1 = 5\)
Start at 0 and make one jump of size 5 (0 → 5).
The result is 5, showing that multiplying by 1 does not change the number.
- Commutative property:
Rule: \(a × b = b × a\)
Multiplication is commutative, meaning that changing the order of the numbers does not affect the result.
Example on a Number Line:
3 × 4 → Start at 0, make 3 jumps of size 4 (0 → 4 → 8 → 12)
4 × 3 → Start at 0, make 4 jumps of size 3 (0 → 3 → 6 → 9 → 12)
Here, both results in 12, proving \(3 × 4 = 4 × 3\).
Explore Our Programs



Representing Multiplication of Numbers on the Number Line
A number line is a line where numbers are spaced evenly. Zero, called the origin, sits right in the middle. Positive numbers go to the right of zero, and negative numbers go to the left. This makes it easy to see both positive and negative numbers in order.
Multiplication of Positive Numbers on a Number Line
Multiplying positive numbers on a number line is simple because it follows the usual multiplication rules. We always move to the right. For example, to calculate 6 × 4, start at zero and make six jumps of 4 units each. After the six jumps, you reach 24, which is the product of 6 × 4.
Multiplication of Negative Numbers on a Number Line
When multiplying negative numbers, we can use the Even-Odd Rule: count the number of negative signs. If there is an even number of negatives, the result is positive. If the number is odd, the result is negative.
For example, to multiply -3 × 7, start at zero and make seven jumps of 3 units each. Since the number is negative, the jumps go to the left on the number line, and you land on -21.
If both numbers are negative, the result becomes positive. For instance, (-5) × (-2) = 10.

Tips and Tricks to Master Multiplication on Number Line
Representing a multiplication on a number line can be confusing sometimes. Here are some tips and tricks to master multiplication on a number line.
- Remember that multiplication is a repeated action. It is as making repeated jumps of the same size on the number line.
- Remember to always start the multiplication from '0'.
- Identify the representation of the numbers. The second number represents the number of jumps to be made.
- Use colors to make learning clearer. Parents and teachers can help children understand number-line multiplication by using colored pencils or markers. Drawing each jump in a different color makes the path easier to follow and adds a fun visual element.
Start with small, simple numbers.
- Parents and teachers can start with easy multiplication facts, such as 2, 3, or 4. Starting small helps children feel confident and makes it easier for them to tackle bigger numbers as they practice more.

Common Mistakes and How to Avoid Them in Multiplication on the Number Line
Students often make mistakes in multiplying numbers on the number line. Here are some few common mistakes made by students:

Real Life Applications of Multiplication on Number Line
The multiplication on the number line has numerous applications across various fields. Let us explore how multiplication on the number line is used in different areas:
- Repeated addition: In many real-life situations, we can use multiplication on a number line like when we buy 4 apples every day for 3 days, on a number line, we make a jump for 4 units 3 times. Which lands on the number line like 0 to 4, 4 to 8 and finally 8 to 12, which is the total number of apples.
- Money calculations: When we are earning 50 rupees per hour and work for 4 hours, on a number line we can start from 0 to take 5 jumps of 50. We will finally land on 200, which is the salary for the work we have done.
- Arranging groups or sets: If a teacher is arranging 6 students per row to make 4 rows, on a number line, starting from 0, we take 4 jumps for 6 units.
- Educational tools: Number lines help in teaching arrays, models, and real-world objects like ceiling tiles or marching soldiers.
- Practical uses: Number lines can help visualize daily situations like calculating spending of repeated meals, grouping objects and so on.

Solved examples on Multiplication on Number Line

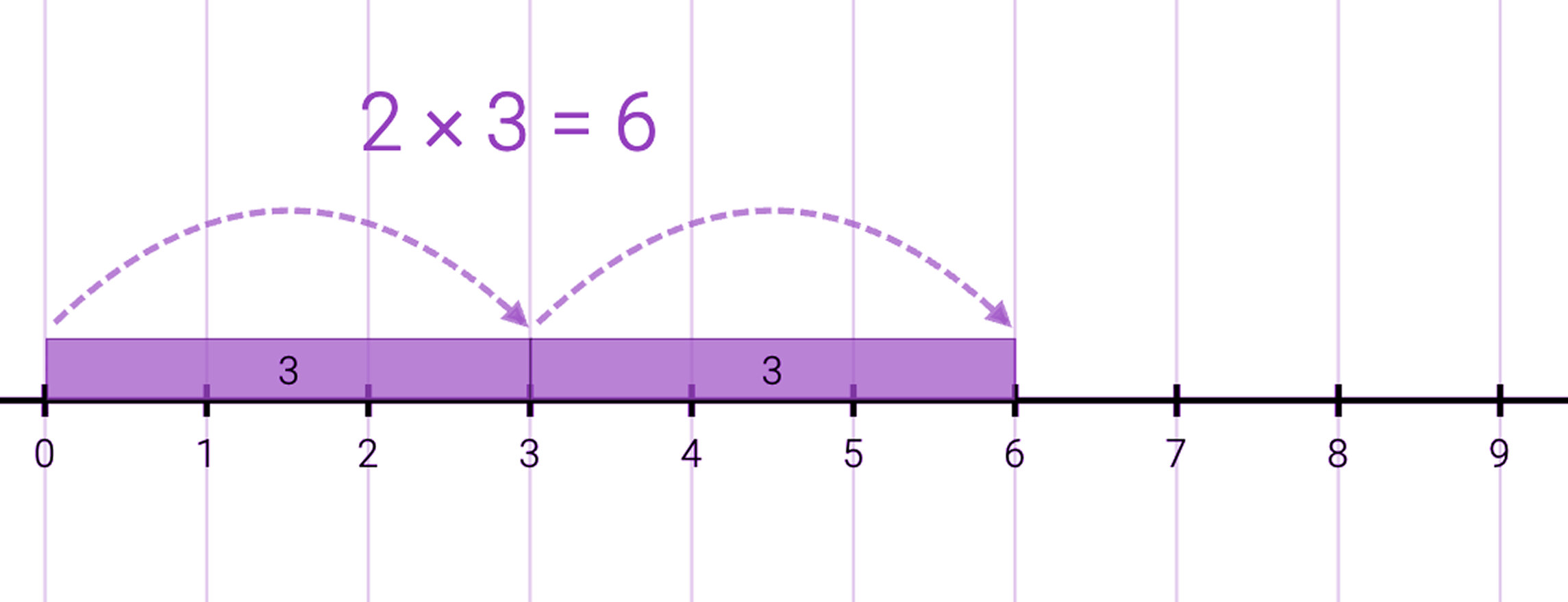
Problem 1
What is 2 × 3?

6
Explanation
Start from 0: Draw a number line beginning at 0.
Determine Jump Size: Each jump represents 3 units.
Make 2 Jumps:
First jump: 0 → 3
Second jump: 3 → 6
Result: The final position is 6.

Problem 2
What is 3 × 4?

12
Explanation
Start at 0: Mark the starting point on the number line.
Each jump is 4 units long.
Make 3 Jumps:
0 → 4
4 → 8
8 → 12
Result: The endpoint is 12.


Problem 3
What is 5 × 2?

10
Explanation
Start at 0: Draw the number line starting at 0.
Determine Jump Size: Each jump represents 2 units.
Make 5 Jumps:
0 → 2
2 → 4
4 → 6
6 → 8
8 → 10
Result: The final number is 10.

Problem 4
What is 4 × 4?

16
Explanation
Start at 0: Begin at zero on the number line.
Determine Jump Size: Each jump equals 4 units.
Make 4 Jumps:
0 → 4
4 → 8
8 → 12
12 → 16
Result: You land on 16.


Problem 5
What is 3 × ½?

1.5
Explanation
Start at 0: Use a number line beginning at 0.
Determine Jump Size: Each jump is \(\frac{1}{2} \) unit.
Make 3 Jumps:
0 → 0.5 (first jump)
0.5 → 1.0 (second jump)
1.0 → 1.5 (third jump)
Result: The endpoint is 1.5.


FAQs on Multiplication on Number Line
1.What is multiplication on a number line?
2.How is multiplication represented on a number line?
3.How do you use a number line to multiply whole numbers?
4.How does the number line help in understanding multiplication?
5.How is repeated addition represented on a number line?
6.How can I explain it to my child easily?
7.What materials can we use at home?
8.How can I help my child practice this daily?


Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.





















