357 LearnersLast updated on May 26th, 2025
Factors of 50
Factors of any number are the whole numbers that can divide the number completely. Why are factors important to learn? For mathematical approaches, factors are used in organizing and bringing more efficiency to any task. In this article, let's learn how to solve factors 50 easily.
What are the Factors of 50?
Factors of 50 are those numbers that can divide 50 perfectly. The factors of 50 are:
1,2,5,10,25, and 50.
Negative factors of 50: -1, -2, -5, -10, -25, -50
Prime factors of 50: 2,5
Prime factorization of 50: 52×2
The sum of factors of 50: 1+2+5+10+25+50 = 93
How to Find the Factors of 50
For finding factors of 50, we will be learning these below-mentioned methods:
- Multiplication Method
- Division Method
- Prime Factor and Prime Factorization
- Factor Tree
Finding Factors using Multiplication Methods
This particular method often finds the pair of factors which, on multiplication together, produces 50. Let us find the pairs which, on multiplication, yields 50.
1×50=50
2×25=50
5×10=50
From this, we conclude that, factors of 50 are: 1,2,5,10,25, and 50.
Finding Factors using Division Method
The division method finds the numbers that evenly divides the given number 50. To find the factors of 50, we have to divide 50 by all possible natural numbers less than 50 and check.
1,2,5,10,25,50 are the only factors that the number 50 has. So to verify the factors of 50 using the division method, we just need to divide 50 by each factor.
50/1 =50
50/2 =25
50/5=10
50/10=5
50/25=2
50/50=1
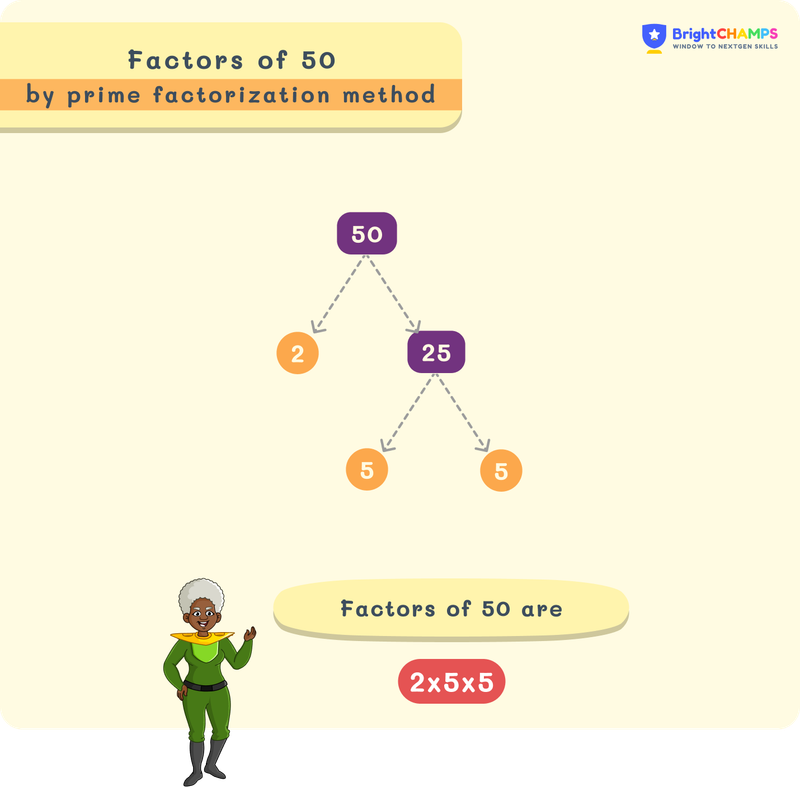
Prime Factors and Prime Factorization
Prime Factorization is the easiest process to find prime factors. It decomposes 50 into a product of its prime integers.
Prime Factors of 50: 2,5.
Prime Factorization of 50: 5×5×2 = 52×2
Factor tree
The number 50 is written on top and two branches are extended.
Fill in those branches with a factor pair of the number above, i.e., 50.
Continue this process until each branch ends with a prime factor (number).
The first two branches of the factor tree of 50 are 2 and 25, then proceeding to 25, we get 5 and 5. So, now the factor tree for 50 is achieved.
Factor Pairs:
Positive pair factors: (1,50), (2,25), and (5,10)
Negative pair factors: (-1,-50), (-2,-25), and (-5,-10).
Common Mistakes and How to Avoid Them in Factors of 50
Children quite often make silly mistakes while solving factors. Let us see what are the common errors to occur and how to avoid them.
Mistake 1
Misconception and confusion about factors with that of multiples.
Factors are way different from multiples. You need to understand it clearly that factors are integers which divide a given number evenly, and multiples are the products we get when the original number is multiplied with different numbers.
Factors of 50 Examples
Problem 1
A baker has 50 cupcakes and 150 cookies. He wants to divide them equally among some plates. What is the maximum number of plates he can use?
Number of cupcakes: 50
Number of cookies: 150
Factors of 50: 1,2,5,10,25,50
Factors of 150: 1,2,3,5,6,10,15,25,30,50,75,150
Common factors of 50 and 150: 1,2,5,10,25,50.
Greatest common factor of 50 and 150: 50
So, there will be 50 plates he can use.
Answer: 50 plates
Explanation
To divide equally, the maximum number of plates can be found through the Greatest Common Factor. Here, we found the GCF, which is the answer.
Problem 2
Two trains leave a station at the same time. One leaves every 25 minutes and the other every 50 minutes. When will they leave together again?
Time-lapse of the 1st train: 25 minutes
Time-lapse of the 2nd train: 50 minutes
Prime factorization of 25: 52.
Prime factorization of 50: 52×2
LCM of 25 and 50: 52×2 = 50.
Both the trains will meet each other after 50 minutes.
Answer: 50 minutes
Explanation
To find the time again when two trains will meet, we have to find the LCM of the two given time-lapses. So, did prime factorization of both 50 and 25. The LCM is the product of the highest power of each factor.
Problem 3
The area of a rectangle is 50 square units. If the length is 10 units, then what is the measure of its width?
Area of rectangle: 50 sq units
Factors of 50: 1,2,5,10,25,50
We know that the area of a rectangle is the product of its length and breadth.
Given, length= 10 units
There exists a factor pair of 50, which is (5,10). Hence, width is 5 units. Let’s check it through the formula for area.
So, length×width = area
⇒ 10 × width = 50
⇒ width = 50/10 = 5
Answer: 5 units
Explanation
Used the concept of factor pairs for 50 and rechecked using the formula for finding area of a rectangle.
Problem 4
Find the smallest number that is divisible by 5,10, and 25.
Prime factorization of 5: 5×1.
Prime factorization of 10: 5×2
Prime factorization of 25: 52
LCM of 5,10 and 25: 52×2 = 50
Answer: 50 is the smallest number which is divisible by 5,10, and 25.
Explanation
To find the smallest number which is divisible by 5,10,25, we need to find the LCM of these numbers.
Problem 5
If a number is divisible by both 2 and 25, is it divisible by 50?
Yes, any number which is divisible by 2 and 25 is also divisible by 50, since 50 = 2×25
Answer: Yes
Explanation
Any number which is divisible by the factor 2 and factor 25 of 50, then it is also divisible by 50 because 50 is a product of 2 and 25.
FAQs on Factors of 50
1.What is the factor tree for 50?
2.What to multiply to get 50?
3. What are the prime factors of 50?
4. What are the multiples of 50?
5.What are all 6 factors of 50?
6.How can children in Thailand use numbers in everyday life to understand Factors of 50?
7.What are some fun ways kids in Thailand can practice Factors of 50 with numbers?
8.What role do numbers and Factors of 50 play in helping children in Thailand develop problem-solving skills?
9.How can families in Thailand create number-rich environments to improve Factors of 50 skills?
Important Glossaries for Factors of 50
- Ratio - Ratio of two numbers compares between them, how many times one number contains the other number. It is expressed as m:n, where m and n are two positive numbers whose ratio is to be shown.
- Factors - These are numbers that divide the given number without leaving any remainder or the remainder as 0.
- Prime Factorization - It involves factoring the number into its prime factors.
- Prime factors - These are the prime numbers which on multiplication together results into the original number whose prime factors are to be obtained.
- Composite numbers - These are numbers having more than two factors.
- Multiple - It is a product of the given number and any other integer.
Explore More numbers
Previous to Factors of 50
About BrightChamps in Thailand
Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.
