449 LearnersLast updated on May 26th, 2025
Factors of 1296
Factors of 1296 are numbers that can divide 1296 completely without leaving any remainder. Understanding factors is useful in various real-life situations, such as organizing items into groups or arranging seating. In this topic, we will explore the factors of 1296 and different methods to find them.
What are the Factors of 1296?
The factors of 1296 are the numbers that divide 1296 evenly.
Those factors are:
Positive Factors of 1296: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 54, 72, 96, 108, 144, 162, 216, 288, 432, 648, and 1296.
Negative Factors of 1296: Negative factors are simply the negative counterparts of the positive factors. These are:
Negative Factors:
-1, -2, -3, -4, -6, -8, -9, -12, -16, -18, -24, -32, -36, -48, -54, -72, -96, -108, -144, -162, -216, -288, -432, -648, and -1296.
Prime Factors of 1296: Prime factors are the prime numbers that, when multiplied together, result in 1296.
Prime Factors of 1296: 2, 3.
Prime Factorization of 1296: Prime factorization is the process of breaking down 1296 into its prime factors.
It is expressed as 2⁴ × 3⁴
Table listing the factors of 1296:
|
Positive Factors |
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 54, 72, 96, 108, 144, 162, 216, 288, 432, 648, 1296 |
|
Negative Factors |
-1, -2, -3, -4, -6, -8, -9, -12, -16, -18, -24, -32, -36, -48, -54, -72, -96, -108, -144, -162, -216, -288, -432, -648, -1296 |
|
Prime Factors |
2, 3 |
|
Prime Factorization |
2⁴ × 3⁴ |
This breakdown helps in understanding the various factors of 1296, whether they are positive or negative, as well as how prime factorization works for this number.
How to Find the Factors of 1296?
There are different methods to find the factors of 1296. Below are some of the common methods:
Methods to Find the Factors of 1296:
- Multiplication Method
- Division Method
- Prime Factorization
- Factor Tree
Finding Factors Using the Multiplication Method
The multiplication method involves finding pairs of numbers whose product is 1296.
Step 1: Find the pair of numbers whose product is 1296.
Step 2: The factors are those numbers that, when multiplied, give 1296.
Step 3: Make a list of numbers whose product will be 1296.
Here are some pairs of numbers whose product is 1296:
1 × 1296 = 1296
2 × 648 = 1296
3 × 432 = 1296
4 × 324 = 1296
6 × 216 = 1296
8 × 162 = 1296
9 × 144 = 1296
12 × 108 = 1296
16 × 81 = 1296
18 × 72 = 1296
24 × 54 = 1296
Thus, the factors of 1296 are:
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54, 72, 81, 108, 144, 162, 216, 324, 432, 648, 1296.
Finding Factors Using the Division Method
The division method finds the numbers that fully divide 1296.
Step 1: Since every number is divisible by 1, 1 will always be a factor. Example: 1296 ÷ 1 = 1296.
Step 2: Move to the next integers, checking for divisibility. Both the divisor and quotient are factors.
Picture showing the division method:
For example:
1296 ÷ 2 = 648 (So, 2 and 648 are factors)
1296 ÷ 3 = 432 (So, 3 and 432 are factors)
Continue until you have checked all integers up to √1296 ≈ 36.
Thus, the factors of 1296 are:
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54, 72, 81, 108, 144, 162, 216, 324, 432, 648, 1296.
Prime Factors and Prime Factorization
Multiplying prime numbers to get the given number as their product is called prime factors. Prime factorization is breaking down the number into its prime factors.
The prime factors of 1296 are 2 and 3.
Steps for Prime Factorization:
Divide 1296 by the smallest prime number, 2:
1296 ÷ 2 = 648
648 ÷ 2 = 324
324 ÷ 2 = 162
162 ÷ 2 = 81 (81 is not divisible by 2, so move to the next prime number, 3)
81 ÷ 3 = 27
27 ÷ 3 = 9
9 ÷ 3 = 3
3 ÷ 3 = 1
Prime Factorization of 1296:
1296 = 2⁴ × 3⁴
Factor Tree
A factor tree visually represents the prime factorization. It helps to understand the factorization process easily.
Here’s how you break down 1296 into its prime factors using a factor tree:
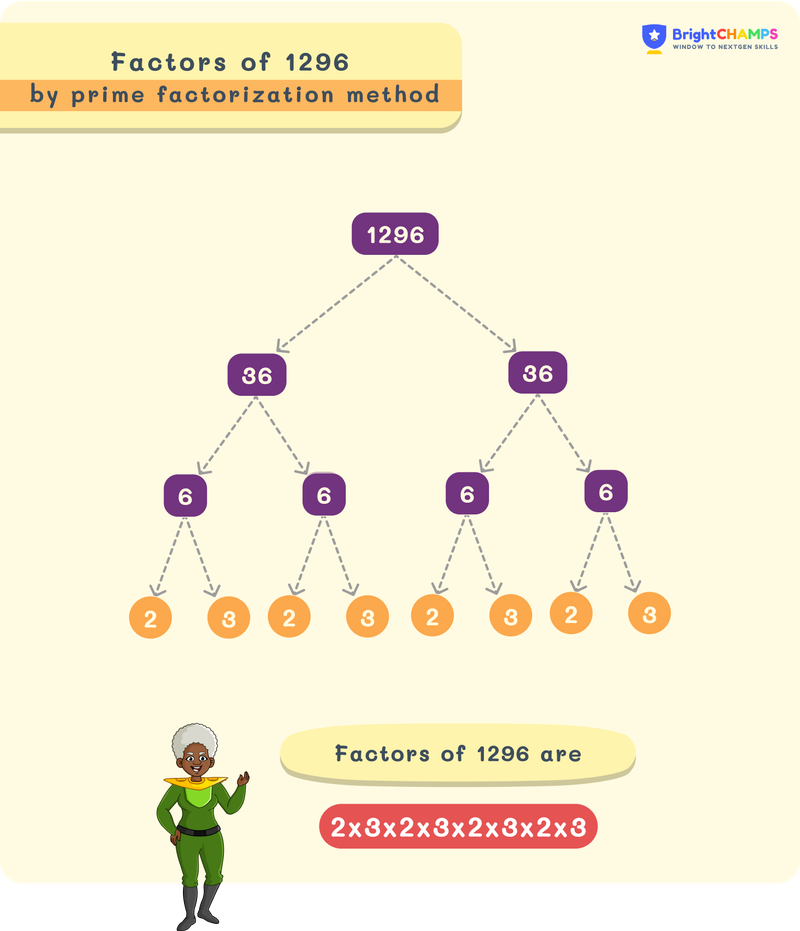
Factors of 1296 can be written in both positive pairs and negative pairs. They are like team members. Their product will be equal to the number given.
Positive Factor Pairs of 1296:
(1, 1296), (2, 648), (3, 432), (4, 324), (6, 216), (8, 162), (9, 144), (12, 108), (16, 81), (18, 72), (24, 54), (36, 36)
Negative Factor Pairs of 1296:
(-1, -1296), (-2, -648), (-3, -432), (-4, -324), (-6, -216), (-8, -162), (-9, -144), (-12, -108), (-16, -81), (-18, -72), (-24, -54), (-36, -36)
These are the positive and negative factor pairs of 1296.
Common Mistakes and How to Avoid Them in Factors of 1296
When finding the factors of 1296, it's easy to make mistakes. Below are some common errors and solutions to help you avoid them while finding the factors of 1296.
Mistake 1
Overlooking the Divisibility Rules for 2 and 3
When finding the factors of 1296, it's important to apply the divisibility rules. For example, 1296 is an even number, so it is divisible by 2. Additionally, checking for divisibility by 3 is crucial—add the digits of 1296 (1 + 2 + 9 + 6 = 18), and since 18 is divisible by 3, 1296 is divisible by 3. Always remember to check divisibility for small prime numbers like 2 and 3 before moving on to larger divisors.
Factors of 75 Examples
Problem 1
If 1296 is divided by 9, how much does each share get?
1296 is divided by 9.
1296 ÷ 9 = 144.
Thus, each share gets 144 when 1296 is divided by 9.
Explanation
To divide 1296 by 9, perform the division step-by-step. The result is a whole number, indicating an equal share of 144 for each part.
Problem 2
Determine the square root of 1296.
The square root of 1296 is 36.
Explanation
36 × 36 = 1296. Thus, the square root of 1296 is 36.
Problem 3
Can 1296 be divided evenly by 72?
To check if 1296 is divisible by 72, divide 1296 by 72.
1296 ÷ 72 = 18, which is an integer.
Explanation
A number is evenly divisible by another if the result of the division is a whole number with no remainder. Here, 1296÷72=181296 \div 72 = 181296÷72=18, which confirms divisibility.
Problem 4
What is the greatest common divisor (GCD) of 1296 and 864?
The greatest of these is 432.
Explanation
The GCD of 1296 and 864 can be found by listing the factors of both numbers.
The common factors of 1296 and 864 are: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 54, 72, 96, 108, 144, 192, 288, 432.
The greatest of these is 432.
Thus, the GCD of 1296 and 864 is 432.
FAQs on Factors of 1296
1.What are the factors of 1296?
2.How do you determine if a number is a factor of 1296?
3.What is the smallest factor of 1296?
4.What is the largest factor of 1296?
5.How many factors does 1296 have?
6.How many odd factors does 1296 have?
7.What factors go into 1296?
8.How many factors of 1296 are perfect squares?
9.How can children in Canada use numbers in everyday life to understand Factors of 1296?
10.What are some fun ways kids in Canada can practice Factors of 1296 with numbers?
11.What role do numbers and Factors of 1296 play in helping children in Canada develop problem-solving skills?
12.How can families in Canada create number-rich environments to improve Factors of 1296 skills?
Important glossaries for the Factors of 1296
Co-prime: Numbers having 1 as the only common factor.
Perfect Square: The number we get when the same number is multiplied twice.
Prime Factors: Prime numbers, which are factors of a given number
Factor Tree: A tree diagram used to represent the prime factors of a given number.
Multiple: Numbers we get when another number multiplies the given number.
Explore More numbers
Previous to Factors of 1296
About BrightChamps in Canada
Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.
