Summarize this article:
 167 Learners
167 LearnersLast updated on August 5, 2025
1/300 as a Decimal

It is a simple question on decimal conversion. Firstly, we have to learn fractions and decimals. A fraction represents a part from the whole. It has two parts: the numerator (number on the top) here, 1 represents how many parts out of the whole. The denominator (number below) shows how many parts make the whole, here it is 300. A decimal is a way to represent the number that is not whole, using a (.) or a decimal to separate the whole part from the fractional part. The numbers to the left of the decimal point represent the whole, and those to the right represent the fractional part.

What is 1/300 as a decimal?
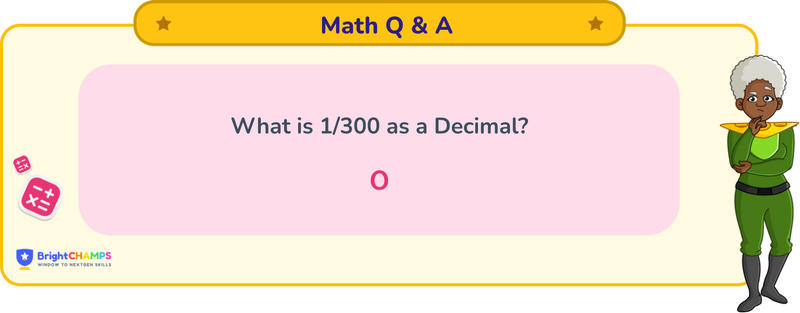
Answer
1/300 in decimals can be written as 0.0033333… It is a recurring decimal, showing it will repeat the same digit infinitely.
Explanation
To get 1/300 in decimal, we will use the division method. Here as 1 is smaller than 300, we will take the help of the decimal method, which will give us 0.0033333… Let's see the step-by-step breakdown of the process:
Step 1: Identify the numerator and denominator because the numerator (1) will be taken as the dividend, and the denominator (300) will be taken as the divisor.
Step 2: As 1 is smaller than 300, it can't be divided. Here, we will take the help of decimals. We will add zeros to the dividend to make it 1000 and add a decimal point in the quotient place.
Step 3: Now that it is 1000, we can divide it by 300. Let's see how many times 300 makes 1000.
Step 4: 1000 is not a multiple of 300, so we will look for the nearest number that is 300 × 3 = 900. We will write 3 in the quotient place and subtract 900 from 1000, which gives 100.
Step 5: Bring down another 0 in the dividend place to make 100 as 1000 and then repeat the division process. The division process continues, and we don't get the remainder as 0. This process is called a recurring decimal.
The answer for 1/300 as a decimal will be 0.0033333…

Important Glossaries for 1/300 as a decimal
- Fraction: A numerical quantity that is not a whole number, representing a part of a whole.
- Decimal: A number that uses the base ten and includes a decimal point to separate the whole part from the fractional part.
- Numerator: The top part of a fraction, indicating how many parts of the whole are being considered
- Denominator: The bottom part of a fraction, showing how many parts make up a whole.
- Recurring Decimal: A decimal number with repeating digits after the decimal point.

Explore More math-questions
![Important Math Links Icon]() Previous to 1/300 as a Decimal
Previous to 1/300 as a Decimal
![Important Math Links Icon]() Next to 1/300 as a Decimal
Next to 1/300 as a Decimal





