123 LearnersLast updated on May 26th, 2025
Square Root of -121
The square root is the inverse of squaring a number. When the number is negative, the square root involves imaginary numbers. Here, we will explore the square root of -121, which is relevant in the field of complex numbers and electrical engineering.
What is the Square Root of -121?
The square root of a number is a value that, when multiplied by itself, gives the original number. Since -121 is a negative number, its square root involves an imaginary unit. The square root of -121 is expressed using the imaginary unit \(i\), where \(i = \sqrt{-1}\). Thus, \(\sqrt{-121} = 11i\) because \(11i \times 11i = 121i^2 = -121\).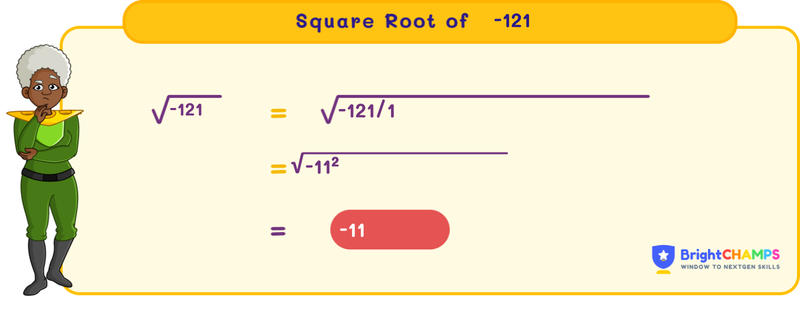
Understanding the Square Root of -121
To find the square root of a negative number, we utilize the concept of imaginary numbers. Imaginary numbers are expressed as multiples of \(i\), where \(i = \sqrt{-1}\). When we square 11i, we get \(-121\), confirming that \(\sqrt{-121} = 11i\).
Properties of Imaginary Numbers
Imaginary numbers have unique properties that differ from real numbers. They are often used in conjunction with real numbers to form complex numbers. Here are some key points about imaginary numbers:
- The square of an imaginary unit \(i\) is \(-1\) (i.e., \(i^2 = -1\)).
- Imaginary numbers can be added, subtracted, multiplied, and divided just like real numbers, but with the additional rules governing \(i\).
- Complex numbers, which are of the form \(a + bi\), where \(a\) and \(b\) are real numbers, are used to represent both real and imaginary numbers.
Applications of Imaginary Numbers
Imaginary and complex numbers are used in various fields such as electrical engineering, control theory, quantum physics, and applied mathematics. They help in solving equations that have no real solutions and in analyzing oscillations, alternating currents, and signal processing.
Common Misconceptions about the Square Root of Negative Numbers
When dealing with square roots of negative numbers, it is crucial to understand that these roots are not real numbers. They represent imaginary numbers and cannot be placed on the real number line. This concept is often misunderstood, leading to errors in calculations and interpretations.
Common Mistakes and How to Avoid Them in the Square Root of -121
Students often make mistakes when dealing with square roots of negative numbers, such as forgetting to use the imaginary unit \(i\), or misunderstanding the nature of complex numbers. Let us explore these common errors in detail.
Mistake 1
Forgetting the Imaginary Unit \(i\)
One of the most common mistakes is neglecting to use the imaginary unit \(i\) when calculating the square root of a negative number. It is essential to remember that \(\sqrt{-121} = 11i\), not just 11.
Square Root of -121 Examples
Problem 1
Find the value of \((\sqrt{-121})^2\).
The value is -121.
Explanation
The square of the square root of a number gives the original number.
Since \(\sqrt{-121} = 11i\), \((11i)^2 = 121i^2 = 121 \times (-1) = -121\).
Problem 2
What is the result of \(\sqrt{-121} + 5\)?
The result is \(5 + 11i\).
Explanation
\(\sqrt{-121}\) is \(11i\), so adding 5 gives \(5 + 11i\), which is a complex number with a real part of 5 and an imaginary part of 11i.
Problem 3
If \(z = \sqrt{-121}\), express \(z^3\) in terms of \(i\).
The expression is \(-1331i\).
Explanation
Given \(z = 11i\), calculate \(z^3 = (11i)^3 = 11^3 \cdot i^3 = 1331 \cdot (-i) = -1331i\) because \(i^3 = i \times i^2 = i \times (-1) = -i\).
Problem 4
Express \(2\sqrt{-121} + 3\sqrt{-121}\) as a single term.
The expression simplifies to \(55i\).
Explanation
Both terms have a common factor of \(\sqrt{-121}\), which is \(11i\).
Therefore, \(2(11i) + 3(11i) = (2 + 3) \times 11i = 5 \times 11i = 55i\).
Problem 5
Simplify \(\sqrt{-121} \times \sqrt{-1}\).
The result is \(-11\).
Explanation
\(\sqrt{-121} = 11i\) and \(\sqrt{-1} = i\).
Multiplying gives \(11i \times i = 11i^2 = 11 \times (-1) = -11\).
FAQ on Square Root of -121
1.What is \(\sqrt{-121}\) in its simplest form?
2.Why is \(\sqrt{-121}\) not a real number?
3.What are the applications of imaginary numbers?
4.How do you represent complex numbers?
5.Does \(\sqrt{-121}\) have a negative counterpart?
Important Glossaries for the Square Root of -121
- Imaginary Unit: The imaginary unit \(i\) is defined as \(\sqrt{-1}\) and is used to express the square roots of negative numbers.
- Complex Number: A complex number consists of a real part and an imaginary part, expressed as \(a + bi\).
- Real Number: A real number is any value that can be found on the number line, including both positive and negative numbers, as well as zero.
- Square of a Complex Number: When a complex number is squared, it involves both real and imaginary components, according to the formula \((a + bi)^2 = a^2 + 2abi - b^2\)."
- Conjugate of a Complex Number: The conjugate of a complex number \(a + bi\) is \(a - bi\), and it is used to simplify division of complex numbers.
Explore More algebra
Previous to Square Root of -121
Jaskaran Singh Saluja
About the Author
Jaskaran Singh Saluja is a math wizard with nearly three years of experience as a math teacher. His expertise is in algebra, so he can make algebra classes interesting by turning tricky equations into simple puzzles.
Fun Fact
: He loves to play the quiz with kids through algebra to make kids love it.
