Summarize this article:
 210 Learners
210 LearnersLast updated on August 5, 2025
Is 1253 a Prime Number?

The numbers that have only two factors, which are 1 and itself, are called prime numbers. For encryption, computer algorithms, barcode generation, prime numbers are used. In this topic, we will be discussing whether 1253 is a prime number or not.

Is 1253 a Prime Number?
There are two types of numbers, mostly — Prime numbers and composite numbers, depending on the number of factors.
A prime number is a natural number that is divisible only by 1 and itself. For example, 3 is a prime number because it is divisible by 1 and itself.
A composite number is a positive number that is divisible by more than two numbers. For example, 6 is divisible by 1, 2, 3, and 6, making it a composite number.
Prime numbers follow a few properties like
Prime numbers are positive numbers always greater than 1.
2 is the only even prime number.
They have only two factors: 1 and the number itself.
Any two distinct prime numbers are co-prime numbers because they have only one common factor that is 1.
As 1253 has only two factors, it is a prime number.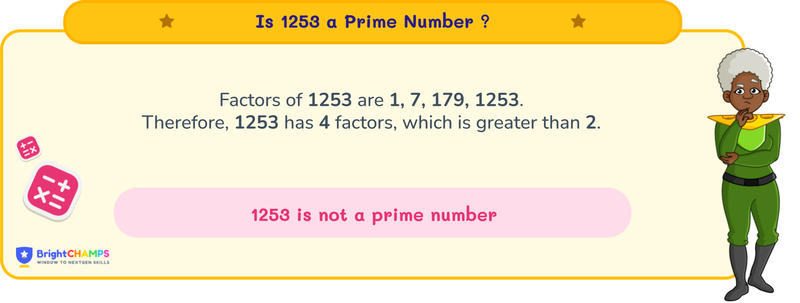

Why is 1253 a Prime Number?
The characteristic of a prime number is that it has only two divisors: 1 and itself. Since 1253 has only two factors, it is a prime number. Few methods are used to distinguish between prime and composite numbers. A few methods are:
- Counting Divisors Method
- Divisibility Test
- Prime Number Chart
- Prime Factorization

Using the Counting Divisors Method
The method in which we count the number of divisors to categorize the numbers as prime or composite is called the counting divisors method. Based on the count of the divisors, we categorize prime and composite numbers.
If there is a total count of only 2 divisors, then the number would be prime.
If the count is more than 2, then the number is composite.
Let’s check whether 1253 is prime or composite.
Step 1: All numbers are divisible by 1 and itself.
Step 2: Divide 1253 by 2. It is not divisible by 2, so 2 is not a factor of 1253.
Step 3: Divide 1253 by 3. It is not divisible by 3, so 3 is not a factor of 1253
Step 4: You can simplify checking divisors up to 1253 by finding the root value. We then need to only check divisors up to the nearest whole number greater than the root value.
Step 5: When we divide 1253 by 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, and 37, we find that none of these divide 1253 evenly.
Since 1253 has only 2 divisors, it is a prime number.
Explore Our Programs



Using the Divisibility Test Method
We use a set of rules to check whether a number is divisible by another number completely or not. It is called the Divisibility Test Method.
Divisibility by 2: The number in the ones' place value is 3. Since 3 is an odd number, 1253 is not divisible by 2.
Divisibility by 3: The sum of the digits in the number 1253 is 11. Since 11 is not divisible by 3, 1253 is not divisible by 3.
Divisibility by 5: The unit’s place digit is 3. Therefore, 1253 is not divisible by 5.
Divisibility by 7, 11, 13, and other primes up to 37: When checking divisibility by these primes, 1253 fails to be divisible by any of them.
Since 1253 is not divisible by any prime numbers other than 1 and itself, it is a prime number.

Using Prime Number Chart
The prime number chart is a tool created by using a method called “The Sieve of Eratosthenes.” In this method, we follow the following steps.
Step 1: Write numbers in a sequential manner.
Step 2: Leave 1 without coloring or crossing, as it is neither prime nor composite.
Step 3: Mark 2 because it is a prime number and cross out all the multiples of 2.
Step 4: Continue marking prime numbers like 3, 5, 7, and cross out their multiples.
Step 5: Repeat this process until you reach numbers beyond the square root of your target number. Through this process, we will have a list of prime numbers.
1253 does not have divisors other than 1 and itself in this list, so it is a prime number.

Using the Prime Factorization Method
Prime factorization is a process of breaking down a number into prime factors. Then multiply those factors to obtain the original number.
Since 1253 cannot be divided evenly by any prime numbers except 1 and itself, it confirms that 1253 is a prime number.

Common Mistakes to Avoid When Determining if 1253 is a Prime Number
Children might have some misconceptions about prime numbers when they are learning about them. Here are some mistakes that might be made by children.

FAQ on is 1253 a Prime Number?
1.Is 1253 a perfect square?
2.What is the sum of the divisors of 1253?
3.What are the factors of 1253?
4.What are the closest prime numbers to 1253?
5.What is the prime factorization of 1253?

Important Glossaries for "Is 1253 a Prime Number"
- Prime number: A natural number greater than 1 that has no positive divisors other than 1 and itself.
- Composite number: A positive integer that has at least one positive divisor other than one or itself.
- Divisibility: A property of integers where one integer can be divided by another with no remainder.
- Sieve of Eratosthenes: An ancient algorithm used to find all prime numbers up to any given limit.
- Prime factorization: Expressing a number as the product of its prime factors.



Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.

















