
 201 Learners
201 LearnersLast updated on May 26th, 2025

2.33333 as a Fraction

Numbers can be categorized into different types. Fraction is one of its kind. It is always represented in the form of p/q, where p is the numerator and q is the denominator. Fraction represents a whole and a fractional part. Decimals represent the fractional part of numbers. For example, 1/2, the numbers in decimal are expressed with a decimal point (.), For example, 2.33333, we are going to learn how to convert a decimal to a fraction.
What is 2.33333 as a Fraction?
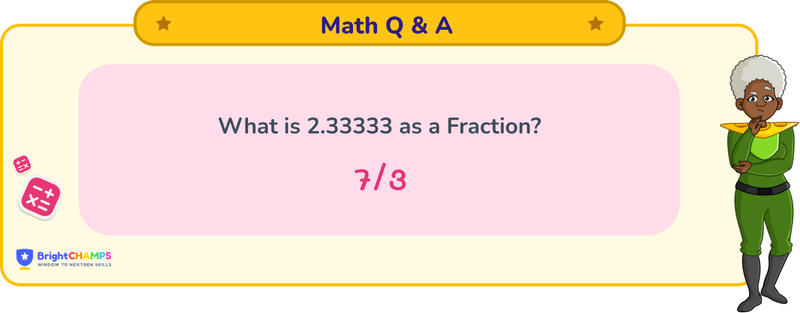
Answer
The answer for 2.33333 as a fraction will be 7/3.
Explanation
Converting a repeating decimal to a fraction involves a few steps. You can follow the steps mentioned below to find the answer.
Step 1: Let x equal the repeating decimal. Here, let x = 2.33333...
Step 2: Multiply by a power of 10 to move the decimal point for one full cycle of repetition. Since the decimal repeats every single digit, multiply by 10. 10x = 23.33333...
Step 3: Subtract the original equation from the new equation to eliminate the repeating part. 10x - x = 23.33333... - 2.33333... 9x = 21
Step 4: Solve for x by dividing both sides by 9. x = 21/9
Step 5: Simplify the fraction by dividing both the numerator and the denominator by their greatest common divisor, which is 3. 21/9 = 7/3
Thus, 2.33333 can be written as a fraction 7/3.
Important Glossaries for 2.33333 as a Fraction
- Fraction: A numerical quantity that is not a whole number, representing a part of a whole.
- Decimal: A number that uses the base ten and includes a decimal point to separate the whole part from the fractional part.
- Repeating Decimal: A decimal in which one or more digits repeat infinitely.
- Numerator: The top part of a fraction, indicating how many parts of the whole are being considered.
- Denominator: The bottom part of a fraction, showing how many parts make up a whole.




