127 LearnersLast updated on May 26th, 2025
Cube Root of 778688
A number we multiply by itself three times to get the original number is its cube root. It has various uses in real life, such as finding the volume of cube-shaped objects and designing structures. We will now find the cube root of 778688 and explain the methods used.
What is the Cube Root of 778688?
We have learned the definition of the cube root. Now, let’s learn how it is represented using a symbol and exponent. The symbol we use to express the cube root is the radical sign (∛), and the exponent we use is ⅓.
In exponential form, ∛778688 is written as 778688(1/3). The cube root is just the opposite operation of finding the cube of a number. For example, assume ‘y’ as the cube root of 778688, then y3 can be 778688. Since the cube root of 778688 is an exact value, it is 92.
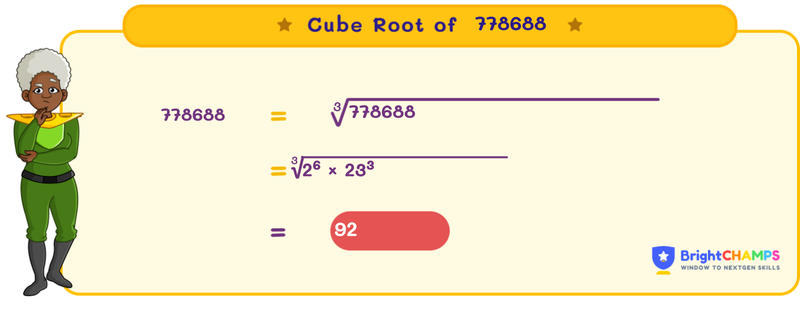
Finding the Cube Root of 778688
Finding the cube root of a number is to identify the number that must be multiplied three times to result in the target number. Now, we will go through the different ways to find the cube root of 778688. The common methods we follow to find the cube root are given below:
- Prime factorization method
- Approximation method
- Subtraction method
- Halley’s method
To find the cube root of a perfect cube number, we often use the prime factorization method. Since 778688 is a perfect cube, we can use this method.
Cube Root of 778688 by Prime Factorization Method
Let's find the cube root of 778688 using the prime factorization method.
Firstly, find the prime factors of 778688.
778688 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 23
We can group the factors into triples: (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × (2 × 2 × 2) × (23)
= 923
Therefore, the cube root of 778688 is 92.
Common Mistakes and How to Avoid Them in the Cube Root of 778688
Finding the cube root of a number without any errors can be a difficult task for the students. This happens for many reasons. Here are a few mistakes the students commonly make and the ways to avoid them:
Mistake 1
Trying to find approximate cube roots for perfect cube numbers.
Children sometimes try to calculate an approximate value for the cube root of numbers like 778688, which are perfect cubes.
For example, they might assume that they need an approximate value like 3.39 for 39. To avoid this error, memorize that perfect cubes have an exact cube root, and the cube root of 778688 is exactly 92.
Mistake 2
Ignoring the exponent form
Most of us might forget the fact that the cube root can also be written in exponent form. For example, forgetting that the cube root of 778688 is 778688^(1/3). To avoid this error, always learn the forms in which we can express the cube root of a number.
Mistake 3
Confusing cube root with division
Assuming the cube root of 778688 is to divide 778688 by 3. For example, mistakenly assume 778688 / 3. To avoid this, children should remember that the cube root of 778688 is the number they multiply by itself three times to get 778688.
Mistake 4
Using approximation methods instead of prime factorization
Instead of using the prime factorization method for perfect cubes, children end up using approximation methods. For example, they might try to find the cube root of 778688 by estimating. Remember that prime factorization is the best method for perfect cubes. Since 778688 is a perfect cube, use the prime factorization method.
Mistake 5
Rounding too early
Rounding the cube root too early in the process can lead to errors in the subsequent steps. However, for perfect cubes like 778688, this isn't a concern as the result is exact. To avoid errors with other calculations, ensure the whole calculation is done, then round the final result if necessary.
Cube Root of 778688 Examples:
Problem 1
Imagine you have a cube-shaped toy that has a total volume of 778688 cubic centimeters. Find the length of one side of the box equal to its cube root.
Side of the cube = ∛778688 = 92 units
Explanation
To find the side of the cube, we need to find the cube root of the given volume. Therefore, the side length of the cube is exactly 92 units.
Problem 2
A company manufactures 778688 cubic meters of material. Calculate the amount of material left after using 100000 cubic meters.
The amount of material left is 678688 cubic meters.
Explanation
To find the remaining material, we need to subtract the used material from the total amount: 778688 - 100000 = 678688 cubic meters.
Problem 3
A bottle holds 778688 cubic meters of volume. Another bottle holds a volume of 5000 cubic meters. What would be the total volume if the bottles are combined?
The total volume of the combined bottles is 783688 cubic meters.
Explanation
Explanation: Let’s add the volume of both bottles: 778688 + 5000 = 783688 cubic meters.
Problem 4
When the cube root of 778688 is multiplied by 2, calculate the resultant value. How will this affect the cube of the new value?
2 × 92 = 184 The cube of 184 = 6229504
Explanation
When we multiply the cube root of 778688 by 2, it results in a new cube root, and its cube results in a substantially larger volume because the cube increases exponentially.
Problem 5
Find ∛(500000 + 278688).
∛(500000 + 278688) = ∛778688 = 92
Explanation
As shown in the question ∛(500000 + 278688), we can simplify that by adding them. So, 500000 + 278688 = 778688. Then we use this step: ∛778688 = 92 to get the answer.
FAQs on 778688 Cube Root
1.Can we find the Cube Root of 778688?
2.Why is the Cube Root of 778688 rational?
3.Is it possible to get the cube root of 778688 as an exact number?
4.Can we find the cube root of any number using prime factorization?
5.Is there any formula to find the cube root of a number?
Important Glossaries for Cube Root of 778688
Cube root: The number that is multiplied three times by itself to get the given number is the cube root of that number. Perfect cube: A number is a perfect cube when it is the product of multiplying a number three times by itself. A perfect cube always results in a whole number. For example, 92 × 92 × 92 = 778688, therefore, 778688 is a perfect cube. Exponent: The exponent form of the number denotes the number of times a number can be multiplied by itself. In 778688^(1/3), ⅓ is the exponent which denotes the cube root of 778688. Radical sign: The symbol that is used to represent a root is expressed as (∛). Rational number: A number that can be expressed as the quotient or fraction of two integers. The cube root of 778688 is rational because it is an exact whole number, 92.
Explore More algebra
Jaskaran Singh Saluja
About the Author
Jaskaran Singh Saluja is a math wizard with nearly three years of experience as a math teacher. His expertise is in algebra, so he can make algebra classes interesting by turning tricky equations into simple puzzles.
Fun Fact
: He loves to play the quiz with kids through algebra to make kids love it.
