Summarize this article:
 227 Learners
227 LearnersLast updated on 5 August 2025
Square Root of 7956

If a number is multiplied by the same number, the result is a square. The inverse of the square is a square root. The square root is used in fields such as vehicle design, finance, etc. Here, we will discuss the square root of 7956.

What is the Square Root of 7956?
The square root is the inverse of the square of a number. 7956 is not a perfect square. The square root of 7956 is expressed in both radical and exponential form. In the radical form, it is expressed as √7956, whereas (7956)^(1/2) in the exponential form. √7956 ≈ 89.1922, which is an irrational number because it cannot be expressed in the form of p/q, where p and q are integers and q ≠ 0.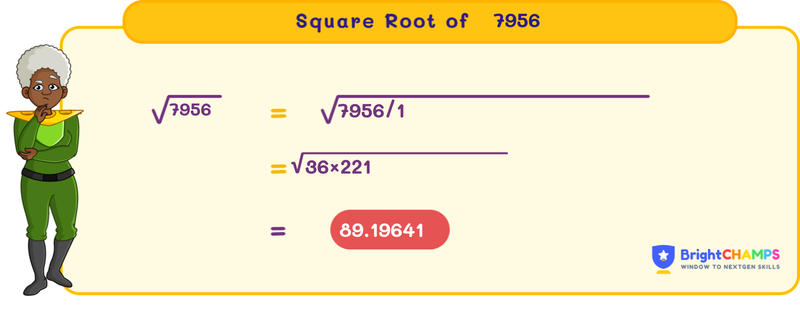

Finding the Square Root of 7956
The prime factorization method is used for perfect square numbers. However, the prime factorization method is not used for non-perfect square numbers where long-division method and approximation method are used. Let us now learn the following methods:
- Prime factorization method
- Long division method
- Approximation method

Square Root of 7956 by Prime Factorization Method
The product of prime factors is the prime factorization of a number. Now let us look at how 7956 is broken down into its prime factors.
Step 1: Finding the prime factors of 7956 Breaking it down, we get 2 × 2 × 3 × 3 × 3 × 37: 2² × 3³ × 37
Step 2: Now we found out the prime factors of 7956. The second step is to make pairs of those prime factors. Since 7956 is not a perfect square, the digits of the number can’t be grouped perfectly into pairs. Therefore, calculating 7956 using prime factorization is challenging without further approximation.

Square Root of 7956 by Long Division Method
The long division method is particularly used for non-perfect square numbers. In this method, we should check the closest perfect square number for the given number. Let us now learn how to find the square root using the long division method, step by step.
Step 1: To begin with, we need to group the numbers from right to left. In the case of 7956, we need to group it as 56 and 79.
Step 2: Now we need to find n whose square is close to or less than 79. We can say n is ‘8’ because 8 × 8 = 64, which is less than or equal to 79. Now the quotient is 8, and after subtracting 79 - 64, the remainder is 15.
Step 3: Now let us bring down 56, which is the new dividend. Add the old divisor with the same number, 8 + 8 = 16, which will be our new divisor.
Step 4: The new divisor will be the sum of the dividend and quotient. Now we get 16n as the new divisor; we need to find the value of n.
Step 5: The next step is finding 16n × n ≤ 1556. Let us consider n as 9, now 16 × 9 = 144.
Step 6: Subtract 1556 from 144, and the difference is 1256, and the quotient is 89.
Step 7: Since the dividend is less than the divisor, we need to add a decimal point. Adding the decimal point allows us to add two zeroes to the dividend. Now the new dividend is 125600.
Step 8: Now we need to find a new divisor that is 892 because 892 × 2 = 1784, which is less than 12560.
Step 9: Subtracting 1784 from 12560, we get the result 10776.
Step 10: Now the quotient is 89.1
Step 11: Continue doing these steps until we get two numbers after the decimal point. Suppose if there are no decimal values, continue until the remainder is zero. So the square root of √7956 is approximately 89.1922.

Square Root of 7956 by Approximation Method
The approximation method is another method for finding square roots. It is an easy method to find the square root of a given number. Now let us learn how to find the square root of 7956 using the approximation method.
Step 1: Now we have to find the closest perfect square of √7956. The smallest perfect square less than 7956 is 7921, and the nearest perfect square greater than 7956 is 8100. √7956 falls somewhere between 89 and 90.
Step 2: Now we need to apply the formula (Given number - smallest perfect square) / (Greater perfect square - smallest perfect square).
Using the formula (7956 - 7921) / (8100 - 7921) = 35 / 179 ≈ 0.1955
Using the formula, we identified the decimal point of our square root.
The next step is adding the value we got initially to the decimal number, which is 89 + 0.1955 ≈ 89.1955, so the square root of 7956 is approximately 89.1955.

Common Mistakes and How to Avoid Them in the Square Root of 7956
Students do make mistakes while finding the square root, such as forgetting about the negative square root, skipping long division methods, etc. Now let us look at a few of those mistakes that students tend to make in detail.

Square Root of 7956 Examples

Problem 1
Can you help Max find the area of a square box if its side length is given as √7956?

The area of the square is approximately 7956 square units.
Explanation
The area of the square = side². The side length is given as √7956. Area of the square = side² = √7956 × √7956 = 7956. Therefore, the area of the square box is approximately 7956 square units.

Problem 2
A square-shaped field measuring 7956 square feet is built; if each of the sides is √7956, what will be the square feet of half of the field?

3978 square feet
Explanation
We can just divide the given area by 2 as the field is square-shaped. Dividing 7956 by 2, we get 3978. So half of the field measures 3978 square feet.

Problem 3
Calculate √7956 × 5.

Approximately 445.961
Explanation
The first step is to find the square root of 7956, which is approximately 89.192. The second step is to multiply 89.192 by 5. So 89.192 × 5 ≈ 445.961.

Problem 4
What will be the square root of (7950 + 6)?

The square root is approximately 89.192.
Explanation
To find the square root, we need to find the sum of (7950 + 6). 7950 + 6 = 7956, and then √7956 ≈ 89.192. Therefore, the square root of (7950 + 6) is approximately ±89.192.

Problem 5
Find the perimeter of the rectangle if its length ‘l’ is √7956 units and the width ‘w’ is 38 units.

We find the perimeter of the rectangle as approximately 254.384 units.
Explanation
Perimeter of the rectangle = 2 × (length + width). Perimeter = 2 × (√7956 + 38) ≈ 2 × (89.192 + 38) = 2 × 127.192 ≈ 254.384 units.


FAQ on Square Root of 7956
1.What is √7956 in its simplest form?
2.Mention the factors of 7956.
3.Calculate the square of 7956.
4.Is 7956 a prime number?
5.7956 is divisible by?
6.How does learning Algebra help students in India make better decisions in daily life?
7.How can cultural or local activities in India support learning Algebra topics such as Square Root of 7956?
8.How do technology and digital tools in India support learning Algebra and Square Root of 7956?
9.Does learning Algebra support future career opportunities for students in India?

Important Glossaries for the Square Root of 7956
- Square root: A square root is the inverse of a square. For example, 4² = 16, and the inverse of the square is the square root, that is √16 = 4.
- Irrational number: An irrational number is a number that cannot be written in the form of p/q, where q is not equal to zero and p and q are integers.
- Principal square root: A number has both positive and negative square roots; however, it is always the positive square root that has more prominence due to its uses in the real world. That is the reason it is also known as a principal square root.
- Prime factorization: Prime factorization is the process of expressing a number as the product of its prime factors. For example, the prime factorization of 18 is 2 × 3².
- Long division method: The long division method is a technique used to find the square root of a non-perfect square by dividing and approximating the root step by step.

Explore More algebra
![Important Math Links Icon]() Previous to Square Root of 7956
Previous to Square Root of 7956
![Important Math Links Icon]() Next to Square Root of 7956
Next to Square Root of 7956

About BrightChamps in India


Jaskaran Singh Saluja
About the Author
Jaskaran Singh Saluja is a math wizard with nearly three years of experience as a math teacher. His expertise is in algebra, so he can make algebra classes interesting by turning tricky equations into simple puzzles.
Fun Fact
: He loves to play the quiz with kids through algebra to make kids love it.




