101 LearnersLast updated on May 26th, 2025
Square of 71
The product of multiplying an integer by itself is the square of a number. Square is used in programming, calculating areas, and so on. In this topic, we will discuss the square of 71.
What is the Square of 71
The square of a number is the product of the number with itself.
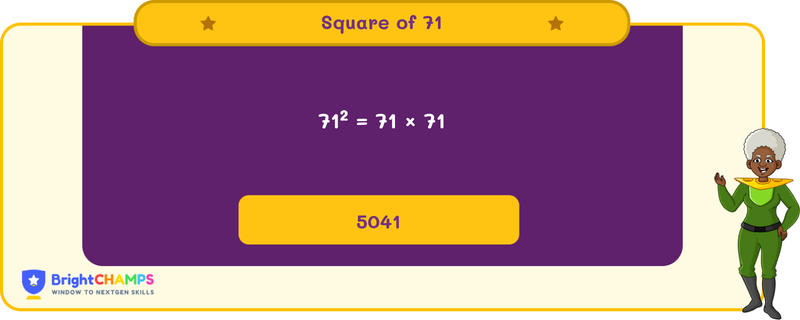
The square of 71 is 71 × 71.
The square of a number can end in 0, 1, 4, 5, 6, or 9.
We write it in math as (712), where 71 is the base and 2 is the exponent.
The square of a positive and a negative number is always positive. For example, (52 = 25); ((-5)2 = 25).
The square of 71 is 71 × 71 = 5041.
Square of 71 in exponential form: (712)
Square of 71 in arithmetic form: 71 × 71
How to Calculate the Value of Square of 71
The square of a number is multiplying the number by itself. So let’s learn how to find the square of a number. These are the common methods used to find the square of a number.
- By Multiplication Method
- Using a Formula (a2)
- Using a Calculator
By the Multiplication Method
In this method, we will multiply the number by itself to find the square.
The product here is the square of the number.
Let’s find the square of 71.
Step 1: Identify the number. Here, the number is 71
Step 2: Multiplying the number by itself, we get, 71 × 71 = 5041.
The square of 71 is 5041.
Using a Formula(a^2)
In this method, the formula, \(a^2\) is used to find the square of the number, where \(a\) is the number.
Step 1: Understanding the equation. Square of a number = (a2) \(a2 = a × a)
Step 2: Identifying the number and substituting the value in the equation.
Here, ‘a’ is 71
So: (712 = 71 × 71 = 5041)
By Using a Calculator
Using a calculator to find the square of a number is the easiest method. Let’s learn how to use a calculator to find the square of 71.
Step 1: Enter the number in the calculator. Enter 71 in the calculator.
Step 2: Multiply the number by itself using the multiplication button (×). That is 71 × 71
Step 3: Press the equal to button to find the answer. Here, the square of 71 is 5041.
Tips and Tricks for the Square of 71
Tips and tricks make it easy for students to understand and learn the square of a number.
- To master the square of a number, these tips and tricks will help students.
- The square of an even number is always an even number. For example, (62 = 36)
- The square of an odd number is always an odd number. For example, (52 = 25)
- The last digit of the square of a number is always 0, 1, 4, 5, 6, or 9.
- If the square root of a number is a fraction or a decimal, then the number is not a perfect square. For example, (sqrt{1.44} = 1.2)
- The square root of a perfect square is always a whole number. For example, (sqrt{144} = 12).
Common Mistakes to Avoid When Calculating the Square of 71
Mistakes are common among kids when doing math, especially when it is finding the square of a number. Let’s learn some common mistakes to master the squaring of a number.
Mistake 1
Calculation errors:
Calculation errors mostly happen when students skip the steps or else by swapping the digits. To avoid it, students should double-check the answer. They can double-check by finding the square root of the solution they found.
For example, the square of 25 is 625, and the square root of 625 is ±25.
Solved Examples on Square of 71
Problem 1
Find the length of the square, where the area of the square is 5041 cm².
The area of a square = (a2)
So, the area of a square = 5041 cm²
So, the length = (sqrt{5041} = 71).
The length of each side = 71 cm
Explanation
The length of a square is 71 cm.
Because the area is 5041 cm², the length is (sqrt{5041} = 71).
Problem 2
Anna wants to tile her square kitchen floor with a side length of 71 feet. The cost to tile a square foot is 5 dollars. How much will it cost to tile the full floor?
The length of the floor = 71 feet
The cost to tile 1 square foot of floor = 5 dollars.
To find the total cost to tile, we find the area of the floor,
Area of the floor = area of the square = (a2)
Here (a = 71)
Therefore, the area of the floor = (712 = 71 × 71 = 5041).
The cost to tile the floor = 5041 × 5 = 25205.
The total cost = 25205 dollars
Explanation
To find the cost to tile the floor, we multiply the area of the floor by the cost to tile per foot. So, the total cost is 25205 dollars.
Problem 3
Find the area of a circle whose radius is 71 meters.
The area of the circle = 15824.06 m²
Explanation
The area of a circle = (pi r2)
Here, (r = 71)
Therefore, the area of the circle = (pi × 712) = (3.14 × 71 × 71 = 15824.06) m².
Problem 4
The area of the square is 5041 cm². Find the perimeter of the square.
The perimeter of the square is 284 cm.
Explanation
The area of the square = (a2)
Here, the area is 5041 cm²
The length of the side is (sqrt{5041} = 71)
Perimeter of the square = 4a Here, (a = 71)
Therefore, the perimeter = 4 × 71 = 284 cm.
Problem 5
Find the square of 72.
The square of 72 is 5184.
Explanation
The square of 72 is multiplying 72 by 72.
So, the square = 72 × 72 = 5184
FAQs on Square of 71
1.What is the square of 71?
2.What is the square root of 71?
3.Is 71 a prime number?
4.What are the first few multiples of 71?
5.What is the square of 70?
6.How does learning Algebra help students in India make better decisions in daily life?
7.How can cultural or local activities in India support learning Algebra topics such as Square of 71?
8.How do technology and digital tools in India support learning Algebra and Square of 71?
9.Does learning Algebra support future career opportunities for students in India?
Important Glossaries for Square of 71.
- Prime number: A number that is only divisible by 1 and itself, such as 2, 3, 5, 7, 11, etc.
- Exponential form: A way of writing numbers using powers, e.g., (92) where 9 is the base and 2 is the exponent.
- Square root: The operation inverse to squaring, finding a number which, when multiplied by itself, gives the original number.
- Perfect square: A number that is the square of an integer, such as 16 (since (42 = 16).
- Multiplication method: Calculating the square by directly multiplying the number by itself.
Explore More algebra
Previous to Square of 71
About BrightChamps in India
Jaskaran Singh Saluja
About the Author
Jaskaran Singh Saluja is a math wizard with nearly three years of experience as a math teacher. His expertise is in algebra, so he can make algebra classes interesting by turning tricky equations into simple puzzles.
Fun Fact
: He loves to play the quiz with kids through algebra to make kids love it.
