Summarize this article:
 1742 Learners
1742 LearnersLast updated on 5 August 2025
Odd Numbers 1 to 1000

Odd numbers are not divisible by 2. Odd numbers leave a remainder of 1, while divided by 2. The voting system with odd numbers of voters will always ensure a definite result. Here, in this topic, we will learn about odd numbers 1 to 1000.

Odd Numbers 1 to 1000
In a simple way, odd numbers are not multiples of 2. In this article, we will learn of those odd numbers lying between 1 and 1000. There are a total of 500 odd numbers lying in this range, where 1 is the smallest and 999 is the largest odd number.

Odd Numbers 1 to 1000 Chart
The odd numbers chart helps you to understand the odd numbers between 1 and 1000. These charts will help you to learn odd numbers using patterns and practice by counting. Take a look at the list of odd numbers and its charts for a better understanding.
Odd Numbers from 1 to 250

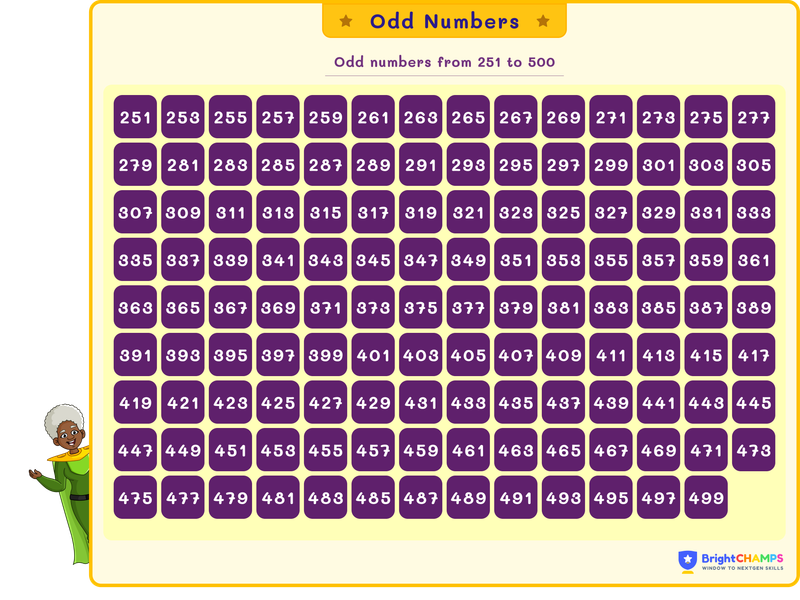
Odd Numbers from 251 to 500
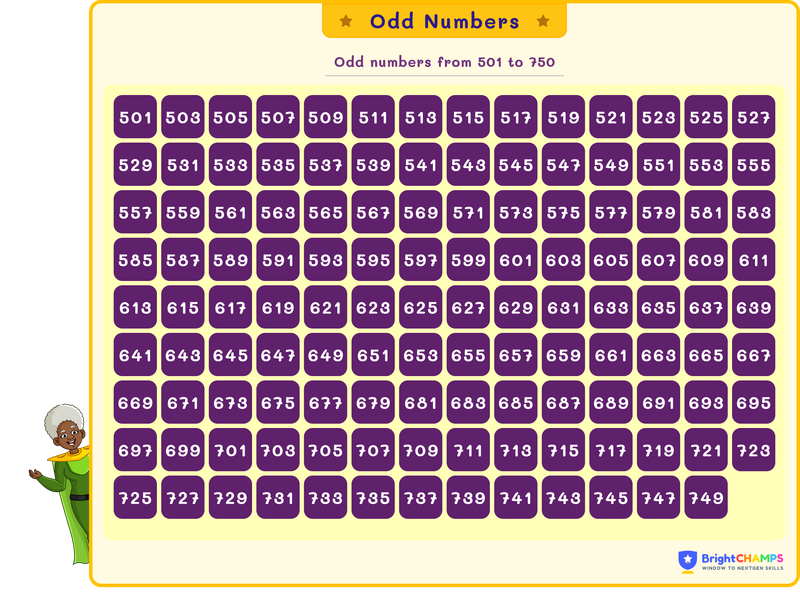
Odd Numbers from 501 to 750
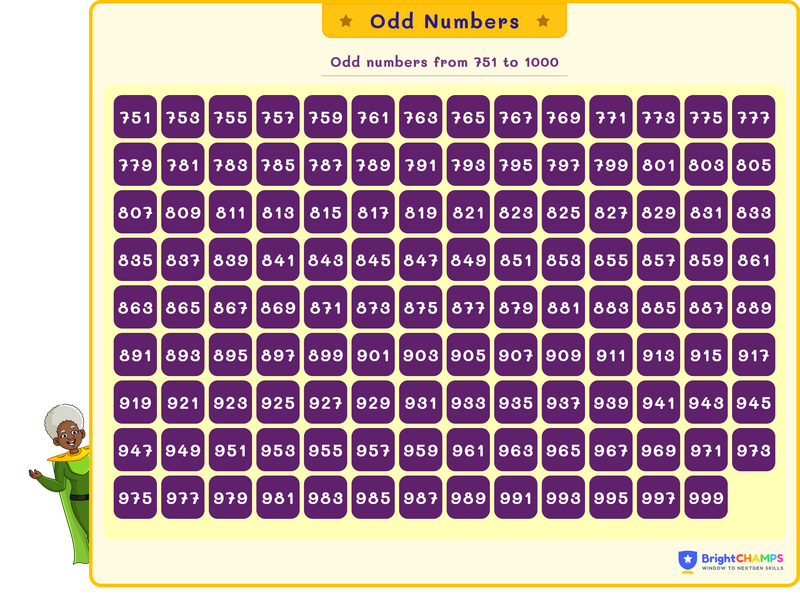
Odd Numbers from 751 to 1000

List of Odd Numbers 1 to 1000
Numbers cannot be odd and even. Odd numbers between 1 and 10000 are 1, 3, 5, 7, 9, 11, 13,......, up to 999 with a common difference of 2 between 2 odd numbers. All these numbers cannot be divided into pairs or equal halves. The numbers from 1 to 1000 consist of 500 odd numbers. Let’s look into the list of odd numbers and their charts given below:
| List of Odd Numbers | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
| 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 |
| 37 | 39 | 41 | 43 | 45 | 47 | 49 | 51 | 53 |
| 55 | 57 | 59 | 61 | 63 | 65 | 67 | 69 | 71 |
| 73 | 75 | 77 | 79 | 81 | 83 | 85 | 87 | 89 |
| 91 | 93 | 95 | 97 | 99 | 101 | 103 | 105 | 107 |
| 109 | 111 | 113 | 115 | 117 | 119 | 121 | 123 | 125 |
| 127 | 129 | 131 | 133 | 135 | 137 | 139 | 141 | 143 |
| 145 | 147 | 149 | 151 | 153 | 155 | 157 | 159 | 161 |
| 163 | 165 | 167 | 169 | 171 | 173 | 175 | 177 | 179 |
| 181 | 183 | 185 | 187 | 189 | 191 | 193 | 195 | 197 |
| 199 | 201 | 203 | 205 | 207 | 209 | 211 | 213 | 215 |
| 217 | 219 | 221 | 223 | 225 | 227 | 229 | 231 | 233 |
| 235 | 237 | 239 | 241 | 243 | 245 | 247 | 249 | 251 |
| 253 | 255 | 257 | 259 | 261 | 263 | 265 | 267 | 269 |
| 271 | 273 | 275 | 277 | 279 | 281 | 283 | 285 | 287 |
| 289 | 291 | 293 | 295 | 297 | 299 | 301 | 303 | 305 |
| 307 | 309 | 311 | 313 | 315 | 317 | 319 | 321 | 323 |
| 325 | 327 | 329 | 331 | 333 | 335 | 337 | 339 | 341 |
| 343 | 345 | 347 | 349 | 351 | 353 | 355 | 357 | 359 |
| 361 | 363 | 365 | 367 | 369 | 371 | 373 | 375 | 377 |
| 379 | 381 | 383 | 385 | 387 | 389 | 391 | 393 | 395 |
| 397 | 399 | 401 | 403 | 405 | 407 | 409 | 411 | 413 |
| 415 | 417 | 419 | 421 | 423 | 425 | 427 | 429 | 431 |
| 433 | 435 | 437 | 439 | 441 | 443 | 445 | 447 | 449 |
| 451 | 453 | 455 | 457 | 459 | 461 | 463 | 465 | 467 |
| 469 | 471 | 473 | 475 | 477 | 479 | 481 | 483 | 485 |
| 487 | 489 | 491 | 493 | 495 | 497 | 499 | 501 | 503 |
| 505 | 507 | 509 | 511 | 513 | 515 | 517 | 519 | 521 |
| 523 | 525 | 527 | 529 | 531 | 533 | 535 | 537 | 539 |
| 541 | 543 | 545 | 547 | 549 | 551 | 553 | 555 | 557 |
| 559 | 561 | 563 | 565 | 567 | 569 | 571 | 573 | 575 |
| 577 | 579 | 581 | 583 | 585 | 587 | 589 | 591 | 593 |
| 595 | 597 | 599 | 601 | 603 | 605 | 607 | 609 | 611 |
| 613 | 615 | 617 | 619 | 621 | 623 | 625 | 627 | 629 |
| 631 | 633 | 635 | 637 | 639 | 641 | 643 | 645 | 647 |
| 649 | 651 | 653 | 655 | 657 | 659 | 661 | 663 | 665 |
| 667 | 669 | 671 | 673 | 675 | 677 | 679 | 681 | 683 |
| 685 | 687 | 689 | 691 | 693 | 695 | 697 | 699 | 701 |
| 703 | 705 | 707 | 709 | 711 | 713 | 715 | 717 | 719 |
| 721 | 723 | 725 | 727 | 729 | 731 | 733 | 735 | 737 |
| 739 | 741 | 743 | 745 | 747 | 749 | 751 | 753 | 755 |
| 757 | 759 | 761 | 763 | 765 | 767 | 769 | 771 | 773 |
| 775 | 777 | 779 | 781 | 783 | 785 | 787 | 789 | 791 |
| 793 | 795 | 797 | 799 | 801 | 803 | 805 | 807 | 809 |
| 811 | 813 | 815 | 817 | 819 | 821 | 823 | 825 | 827 |
| 829 | 831 | 833 | 835 | 837 | 839 | 841 | 843 | 845 |
| 847 | 849 | 851 | 853 | 855 | 857 | 859 | 861 | 863 |
| 865 | 867 | 869 | 871 | 873 | 875 | 877 | 879 | 881 |
| 883 | 885 | 887 | 889 | 891 | 893 | 895 | 897 | 899 |
| 901 | 903 | 905 | 907 | 909 | 911 | 913 | 915 | 917 |
| 919 | 921 | 923 | 925 | 927 | 929 | 931 | 933 | 935 |
| 937 | 939 | 941 | 943 | 945 | 947 | 949 | 951 | 953 |
| 955 | 957 | 959 | 961 | 963 | 965 | 967 | 969 | 971 |
| 973 | 975 | 977 | 979 | 981 | 983 | 985 | 987 | 989 |
| 991 | 993 | 995 | 997 | 999 | ||||

Sum of Odd Numbers 1 to 1000
We can calculate the sum of all odd numbers from 1 to 1000 using the formula S = n/2 (first odd number + last odd number), where n is the total count of odd numbers within 1 to 1000. As there are 500 odd numbers (n = 500) between 1 and 1000, we can substitute these values into the formula
S = n/2 (first odd number + last odd number)
S = 500/2 (1+999)
This simplifies to:
S = 250 x 1000
S = 250,000
Therefore, we get the sum as 250,000 odd numbers between 1 and 1000.

Subtraction of Odd Numbers 1 to 1000
Subtracting two odd numbers results in even numbers. While subtracting an odd number from an even number results in an odd number. For example, If you subtract 10 - 3, you get 7 which is an odd number. Whereas, subtracting an odd number from an odd number will always result in an even number. For example, 7 - 3 you get 4, which is an even number.

Odd Prime Numbers 1 to 1000
We know that except 2 all the other prime numbers are odd numbers. However, not all odd numbers are prime numbers. For example, 15, 21, 25, etc, are odd numbers but not prime numbers. It cannot be an odd number, because it has more than two factors other than 1 and the number itself. The smallest odd prime number is 3.

Odd Numbers 1 to 1000 Examples

Problem 1
How many odd numbers are there between 1 and 1000?

There are 500 odd numbers.
Explanation
Odd numbers between 1 and 1000 form an arithmetic sequence like 1, 3, 5,....999.
The total count is given by (last term – first term) divided by the common difference + 1. That is,
(last term - first term) ÷ Common Difference + 1
(999 – 1) ÷ 2 + 1 = 500.

Problem 2
What is the sum of all odd numbers between 1 and 1000?

The sum is 250,000
Explanation
The sum of the first n odd numbers given by n2. There are 500 odd numbers, so 5002 which is equal to 250,000

Problem 3
What is the largest odd number between 1 and 1000?

The largest odd number is 999
Explanation
Odd numbers alternate with even numbers. Since 1000 is even, the largest odd number, it is 999.

Problem 4
What is the difference between two consecutive odd numbers?

The difference is always 2.
Explanation
The common difference between two consecutive odd numbers is always 2 in an arithmetic sequence, e.g., 1, 3, 5, etc.

Problem 5
Imagine that you have 15 candies, and want to share them with your 3 friends so that everyone gets an odd number of candies. Is it possible?

Yes, it is possible.
Explanation
So, given that the total number of candies is 15.
Number of friends = 3
If you divide the number of candies by the number of friends, you get
The odd number of candies that each will get = No. of candies / No. of Friends
= 15 / 3 = 5
The number of candies each friend will get is 5, which is an odd number.
Therefore, it is possible.


FAQs on Odd Numbers 1 to 1000
1.What are odd numbers?
2.How many odd numbers are there between 1 and 1000?
3.What is the smallest odd number?
4.What is the largest odd number between 1 and 1000?
5.What is the difference between two consecutive odd numbers?
6.What role do numbers and Odd Numbers 1 to 1000 play in helping children in Indonesia develop problem-solving skills?
7.What are some fun ways kids in Indonesia can practice Odd Numbers 1 to 1000 with numbers?
8.How can children in Indonesia use numbers in everyday life to understand Odd Numbers 1 to 1000?
9.How can families in Indonesia create number-rich environments to improve Odd Numbers 1 to 1000 skills?

Important Glossaries for Odd Numbers 1 to 1000
- Odd Numbers: Integers that cannot be evenly divided by 2 are odd numbers. For example, 1, 3, 5, etc.
- Prime Numbers: A prime number is an integer greater than one that has no divisors other than 1 and itself, for example, 3 is a prime number because it has 2 factors - 1 and 3 itself.
- Common Difference: Numbers that are added or subtracted with the same amount are called common differences. For example, 3 - 2 = 1, 2 - 1 = 1.

Explore More numbers
![Important Math Links Icon]() Previous to Odd Numbers 1 to 1000
Previous to Odd Numbers 1 to 1000
![Important Math Links Icon]() Next to Odd Numbers 1 to 1000
Next to Odd Numbers 1 to 1000


Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.




