Summarize this article:
 1293 Learners
1293 LearnersLast updated on December 17, 2025
Factors of 63

Factors of 63 are the whole numbers that can divide the number evenly without the remainder. In daily life, unknowingly, we apply factors to divide anything evenly in the group. In this article, we will study different methods to solve and solved examples of factors of 63.

What are the Factors of 63?
The factors of 63 are 1, 3, 7, 9, 21 and 63
Negative Factors
These are negative counterparts of the positive factors.
Negative factors: -1, -3, -7, -9, -21, -63
Prime Factors
Prime factors are the prime numbers themselves, when multiplied together, give 63 as the product.
Prime factors: 3, 7
Prime Factorization
Prime factorization involves breaking 63 into its prime factors
It is expressed as 32 × 71
The factors of 63 can be written as shown in the table given below:
| Factor | Type Values |
| Positive Factors of 63 | 1, 3, 7, 9, 21, 63 |
| Negative Factors of 63 | −1, −3, −7, −9, −21, −63 |
| Prime Factors of 63 | 3, 7 |
| Prime Factorization of 63 | 3 × 3 × 7 = 3² × 7 |
| The sum of the Factors of 63 | 104 |

How to Find the Factors of 63?
There are different methods to find the factors of 63.
Methods to find the factors of 63:
- Multiplication Method
- Division Method
- Prime Factor and Prime Factorization

Finding Factors Using Multiplication Method
The multiplication method finds the pair of factors that give 63 as their product.
Step-by-step process
Step 1: Find the pair of numbers whose product is 63.
Step 2: The factors are those numbers, when multiplied, give 63.
Step 3: Make a list of numbers whose product will be 63.
A list of numbers whose products are 63 is given below:
1 × 63 = 63
3 × 21 = 63
7 × 9 = 63

Explore Our Programs



Finding Factors Using Division Method
The division method finds the numbers that fully divide the given number.
Step-by-step process:
Step 1: Since every number is divisible by 1, 1 will always be a factor. Example: 63÷1 = 63
Step 2: Move to the next integer. Both divisor and quotient are the factors.
Picture showing the division method:


Prime Factors and Prime Factorization
- Multiplying prime numbers to get the given number as their product is called prime factors.
- Prime factorization is breaking down the number into its prime factors.

Prime Factors of 63
Prime Factors of 63
Number 63 has only one prime factor.
Prime factors of 63: 3, 7
To find the prime factors of 63, divide 63 with the prime numbers 3 and 7.
- 63÷3 = 21
- 21÷3 = 7
- 7÷7 = 1

Prime Factorization of 63
Prime Factorization of 63:
Prime Factorization breaks down the prime factors of 63
Expressed as 32 × 71
Factor Tree
The prime factorization is visually represented using the factor tree. It helps to understand the process easily. In this factor tree, each branch splits into prime factors.
Factor Tree for 63:
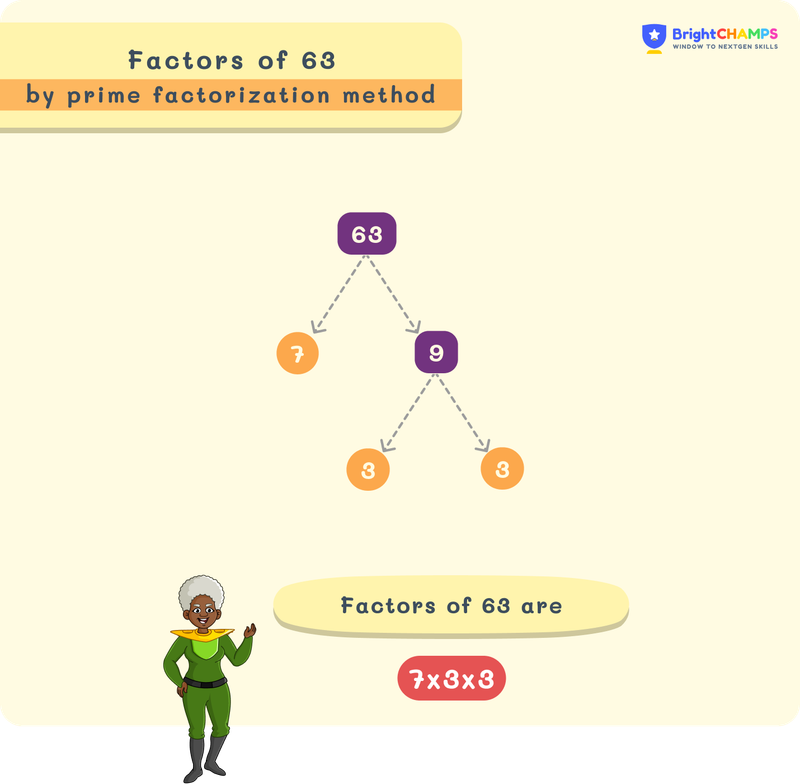

Factor Pairs of 63
The factors of 63 can be written in both positive and negative pairs. The table below represents the factor pairs of 63, where the product of each pair of numbers is equal to 63.
Positive Pair Factors of 63:
| Factors | Positive Pair Factors |
| 1 × 63 = 63 | 1, 63 |
| 3 × 21 = 63 | 3, 21 |
| 7 × 9 = 63 | 7, 9 |
Since the product of two negative numbers is also positive, 63 also has negative pair factors.
Negative Pair Factors of 63:
| Factors | Negative Pair Factors |
| −1 × −63 = 63 | −1, −63 |
| −3 × −21 = 63 | −3, −21 |
| −7 × −9 = 63 | −7, −9 |

Common Mistakes and How to Avoid Them in Factors of 63
Mistakes can occur while finding the factors. Learn about the common errors that can occur. Solutions to solve the common mistakes are given below.

Examples on Factors of 63

Problem 1
If we add all the factors of 63, what will be the sum?

The sum of factors is 104
Explanation
Add all the factors of 63 (1+3+7+9+21+63) to get the sum 104.

Problem 2
Find the sum of the factor pair (7,9) and verify whether the sum is divisible by 2.

The sum of the factor pair (7,9) is 16 and the sum is divisible by 2
Explanation
When the factor pair (7,9) is added (7+9) we get 16 as the sum. To verify whether 16 is divisible by 2, we check if the
remainder is zero when 16 is divided by 2. Here, the remainder is zero. Hence, 16 is divisible by 2.

Problem 3
How many single-digit factors are there for 63?

There are four single-digit factors.
Explanation
Write down the factors 63 and identify the single-digit factors.
The single-digit factors are 1, 3, 7 and 9.

Problem 4
A Costco store in Chicago receives 63 granola bars to be packed equally into gift boxes for a school fundraiser. The manager wants to know all the possible group sizes so that no granola bar is left over. What are all the possible factors of 63 that represent the number of granola bars per box?

1, 3, 7, 9, 21, 63
Explanation
Factors are numbers that divide 63 exactly without leaving a remainder. When 63 granola bars are divided equally, the possible group sizes are 1, 3, 7, 9, 21, and 63. Each of these numbers divides 63 evenly, making them valid factors.

Problem 5
A pharmacist at CVS in Boston has 63 tablets of a vitamin supplement. The tablets must be arranged into equal daily dosage packs for patients, with no tablets left unused. Which numbers can be used as the number of tablets per pack using the factors of 63?

1, 3, 7, 9, 21, 63
Explanation
To find valid dosage pack sizes, we list all the factors of 63. A factor divides 63 exactly. Since 63 can be evenly divided by 1, 3, 7, 9, 21, and 63, each of these values can represent a possible tablets-per-pack option.

Problem 6
An NCAA basketball camp in Dallas has 63 practice cones to distribute equally among training stations. Each station must receive the same number of cones with none left over. How many different ways can the cones be distributed using the factors of 63?

1, 3, 7, 9, 21, 63
Explanation
Equal distribution is possible only when the total number can be divided evenly. The factors of 63 show all possible equal groupings. Since 63 is divisible by 1, 3, 7, 9, 21, and 63, these represent all the valid distribution options.


FAQs on Factors of 63
1.What are the two prime factors of 63?
2.Is 63 a factor of 4?
3.What is the HCF of 27 and 63?
4.Is 7 a factor of 63?
5.What is the GCF of 63 and 81?
6.How many factors does 63 have?
7.What is the smallest factor of 63?
8.What is the largest factor of 63?
9.Which factors of 63 add up to 13?
10.How many even factors does 63 have?
11.What are the odd factors of 63?
12.What is the sum of all the factors of 63?


Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.




























