223 LearnersLast updated on May 26th, 2025
Factors of 1369
Factors of 1369 are numbers that can divide 1369 completely without leaving a remainder. Factors are often used in organizing mathematical concepts and problem-solving. In this topic, we will know more about the factors of 1369 and the different methods to find them.
What are the Factors of 1369?
The factors of 1369 are 1, 37, and 1369.
Positive Factors
Positive factors: 1, 37, 1369
Negative Factors
Negative factors are the negative counterparts of the positive factors.
Negative factors: -1, -37, -1369
Prime Factors
Prime factors are prime numbers that, when multiplied together, give 1369 as the product.
Prime factors: 37
Prime Factorization
Prime factorization involves breaking 1369 into its prime factors.
It is expressed as 372
How to Find the Factors of 1369?
There are different methods to find the factors of 1369.
Methods to Find the Factors of 1369:
- Multiplication Method
- Division Method
- Prime Factorization
- Factor Tree
Finding Factors Using Multiplication
The multiplication method finds the pair of factors that give 1369 as their product.
Steps:
- Find the pair of numbers whose product is 1369.
- The factors are those numbers which, when multiplied, give 1369.
- Make a list of numbers whose product will be 1369.
A list of numbers whose products are 1369 is given below:
1 × 1369 = 1369
37 × 37 = 1369
Thus, the factors of 1369 are 1, 37, and 1369.
Finding Factors by Division Method
The division method finds the numbers that fully divide the given number.
Step 1:Since every number is divisible by 1, 1 will always be a factor.
Example: 1369÷1=1369
Step 2:Move to the next integer. Check divisibility until all possible factors are identified.
Thus, the factors of 1369 are 1, 37, and 1369
Prime Factors and Prime Factorization
Multiplying prime numbers to get the given number as their product is called prime factorization. A number, when simplified using the factors of that number and expressed in the form of prime factors, represents its prime factorization.
Prime Factors of 1369
The number 1369 has only one prime factor.
Prime factors of 1369: 37
To find the prime factors of 1369, divide 1369 with 37:
1369÷37=37
37÷37=1
Prime Factorization of 1369
Prime factorization breaks down the prime factors of 1369:
Expressed as 37×37 or 372
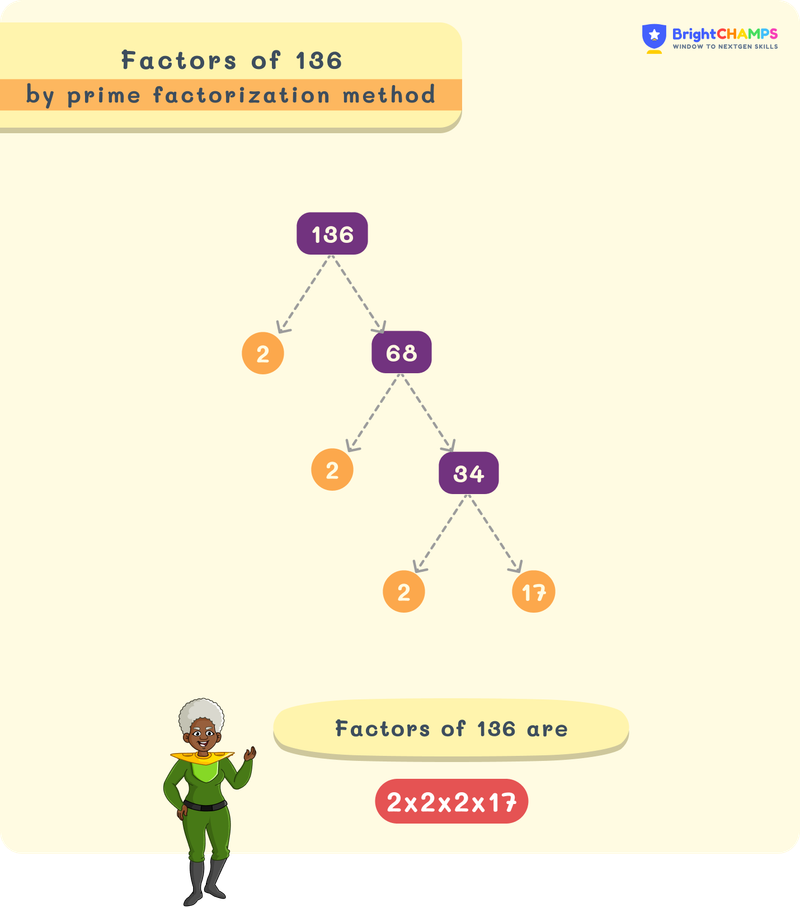
Factor Tree
The prime factorization can be visually represented using a factor tree. It helps to understand the process easily.
This tree shows the breakdown of 1369 into its prime factors: 37×37
Factors of 1369 can also be written in both positive and negative pairs. Their product will always equal the given number.
Positive Factor Pairs:
(1,1369),(37,37)(1, 1369), (37, 37)(1,1369),(37,37)
Negative Factor Pairs:
(−1,−1369),(−37,−37)(-1, -1369), (-37, -37)(−1,−1369),(−37,−37)
Common Mistakes and How to Avoid Them in Factors of 1369
Mistakes can happen when finding the factors of 1369. Below are some common errors and tips on how to avoid them for accurate factor identification.
Mistake 1
Assuming 1 as the only factor of 1369
Factors are numbers that can divide the given number equally. While 1 is a factor, so are 37 and 1369.
Factors of 1369 Examples
Problem 1
Can you check whether 37 and 1369 are co-prime?
No, 37 and 1369 are not co-prime
Explanation
To check whether two numbers are co-prime, list their factors first. Once you have listed the factors, identify the common factors and determine the GCF. If the GCF is greater than 1, then the numbers are not co-prime.
Factors of 37: 1, 37 Factors of 1369: 1, 37, 1369
Here, the GCF is 37. So, 37 and 1369 are not co-prime. For co-prime, the GCF of numbers should be 1.
Problem 2
Verify whether 1369 is a multiple of 37
Yes, 1369 is a multiple of 37
Explanation
Multiples of 37 are numbers that can be obtained by multiplying 37 by whole numbers. Since 37 × 37 = 1369, it is a multiple of 37.
Problem 3
Identify the perfect square from the factors of 1369
The perfect square factor of 1369 is 1369, and the root is 37
Explanation
A perfect square is a number we get when the same number is multiplied by itself. When 37 is multiplied by itself (37 × 37), we get the perfect square 1369.
Problem 4
List all the factors of 1369
The factors of 1369 are 1, 37, and 1369
Explanation
Factors of a number are all the whole numbers that divide that number without leaving a remainder. For 1369, the factors are 1, 37, and 1369.
Problem 5
Is 1369 a prime number?
No, 1369 is not a prime number
Explanation
A prime number has only two factors: 1 and itself. Since 1369 has factors other than 1 and 1369 (specifically, 37), it is not a prime number.
FAQs on Factors of 1369
1.What are the factors of 1369?
2.How do you determine if a number is a factor of 1369?
3.What is the smallest factor of 1369?
4.What is the largest factor of 1369?
5.How many factors does 1369 have?
6.How many odd factors does 1369 have?
7.What factors go into 1369?
8.Do any perfect squares exist in the factors of 1369?
Important glossaries for the Factors of 1369
Factors of 1369: Numbers that can divide 1369 completely without leaving a remainder. The factors of 1369 include 1, 37, and 1369.
Prime Factors: Prime numbers that, when multiplied together, yield 1369. The prime factor of 1369 is 37.
Prime Factorization: The process of breaking 1369 down into its prime factors and expressing it as a product. For 1369, the prime factorization is 37×37
Factor Tree: A visual diagram used to represent the process of finding the prime factors of 1369. It helps illustrate that 1369 can be broken down into 37×37
Perfect Square: A number that results from multiplying the same number by itself. 1369 is a perfect square because 37×37=1369.
Explore More numbers
Previous to Factors of 1369
Hiralee Lalitkumar Makwana
About the Author
Hiralee Lalitkumar Makwana has almost two years of teaching experience. She is a number ninja as she loves numbers. Her interest in numbers can be seen in the way she cracks math puzzles and hidden patterns.
Fun Fact
: She loves to read number jokes and games.
