114 LearnersLast updated on May 26th, 2025
Square Root of -77
When a number is multiplied by itself, the result is a square. The inverse of a square is a square root. The concept of square roots is used in various fields including complex numbers, engineering, and physics. Here, we will discuss the square root of -77.
What is the Square Root of -77?
The square root is the inverse of squaring a number. Since -77 is a negative number, it does not have a real square root. Instead, the square root of -77 is expressed using imaginary numbers. In mathematical terms, it can be represented as √(-77) = √(77) * i, where i is the imaginary unit, defined as √(-1).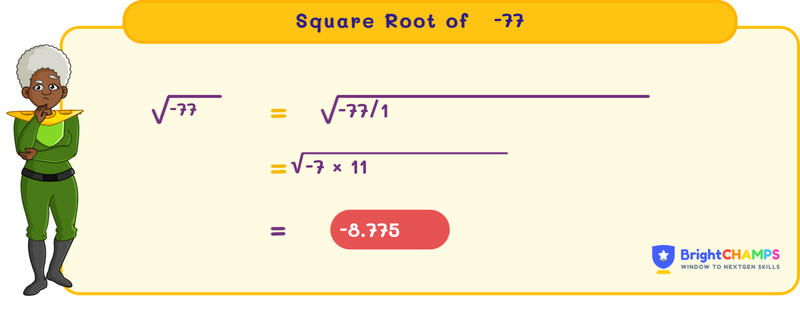
Understanding the Square Root of -77
To find the square root of a negative number like -77, we utilize the concept of imaginary numbers. Imaginary numbers allow us to extend the number system to solve equations that do not have real solutions. The square root of -77 is expressed as an imaginary number (complex number with no real part). The real part of the square root of 77 is approximately 8.775, so √(-77) = 8.775i.
Square Root of -77 by Using Imaginary Numbers
Imaginary numbers are introduced to handle square roots of negative numbers. Here's how we express the square root of -77 using imaginary numbers:
Step 1: Identify the negative sign under the square root.
Step 2: Separate the negative sign as √(-1) which is denoted by i, giving us i√77.
Step 3: Calculate the square root of 77 (approximately 8.775).
Step 4: Express the final result as 8.775i.
Understanding Imaginary Numbers
Imaginary numbers are used for finding solutions to equations that involve the square root of negative numbers, which do not exist in the set of real numbers. They are represented with the imaginary unit i, where i = √(-1). This concept is quite useful in advanced mathematics and physics.
Applications of the Square Root of Negative Numbers
Square roots of negative numbers are used in various scientific fields:
1. Electrical Engineering: For calculating impedance in AC circuits.
2. Signal Processing: For analyzing waves and signals.
3. Quantum Mechanics: For solving equations that describe physical phenomena on a quantum scale.
Common Mistakes and How to Avoid Them with Square Roots of Negative Numbers
Students often make errors when dealing with square roots of negative numbers, such as confusing real and imaginary results or misapplying the imaginary unit. Below are some common mistakes and tips to avoid them.
Mistake 1
Ignoring the Imaginary Component
It's crucial to remember that negative numbers do not have real square roots. Always include the imaginary unit i when expressing square roots of negative numbers.
For example, √(-77) should be expressed as 8.775i, not just 8.775.
Square Root of -77 Examples
Problem 1
Can you help Max find the square of the imaginary unit i?
The square of the imaginary unit i is -1.
Explanation
By definition, i is the square root of -1. Therefore, squaring i gives (√(-1))^2 = -1.
Problem 2
If a complex number is expressed as 3 + √(-77), what is its imaginary component?
8.775i
Explanation
The imaginary component of the complex number 3 + √(-77) is derived from the square root of -77, which is 8.775i.
Problem 3
Calculate 2 * √(-77).
17.55i
Explanation
First, find √(-77) = 8.775i. Then, multiply by 2: 2 * 8.775i = 17.55i.
Problem 4
What would be the result of (√(-77))^2?
-77
Explanation
By definition, squaring the square root of a number returns the original number. Thus, (√(-77))^2 = -77.
Problem 5
A complex number is given by 5 + √(-77). What is its magnitude?
The magnitude is approximately 9.84.
Explanation
Magnitude is calculated as √(real part^2 + imaginary part^2). Here, real part = 5, imaginary part = 8.775. Magnitude = √(5^2 + 8.775^2) = √(25 + 77) = √102 ≈ 9.84.
FAQ on Square Root of -77
1.What is √(-77) in its simplest form?
2.What are imaginary numbers?
3.Why can't we find a real square root of a negative number?
4.How do we express square roots of negative numbers?
5.What is the relation between i and -1?
Important Glossaries for the Square Root of -77
- Imaginary Number: A number that can be expressed in the form of a real number multiplied by the imaginary unit i, where i = √(-1).
- Complex Number: A number that comprises a real part and an imaginary part, typically expressed as a + bi.
- Imaginary Unit: Represented as i, it is the square root of -1 and is used to denote the square roots of negative numbers.
- Magnitude: The distance of a complex number from the origin in the complex plane, calculated as √(real part^2 + imaginary part^2).
- Negative Number: A number less than zero, which does not have a real square root, necessitating the use of imaginary numbers.
Explore More algebra
Previous to Square Root of -77
Jaskaran Singh Saluja
About the Author
Jaskaran Singh Saluja is a math wizard with nearly three years of experience as a math teacher. His expertise is in algebra, so he can make algebra classes interesting by turning tricky equations into simple puzzles.
Fun Fact
: He loves to play the quiz with kids through algebra to make kids love it.
