Square Root of 0.4

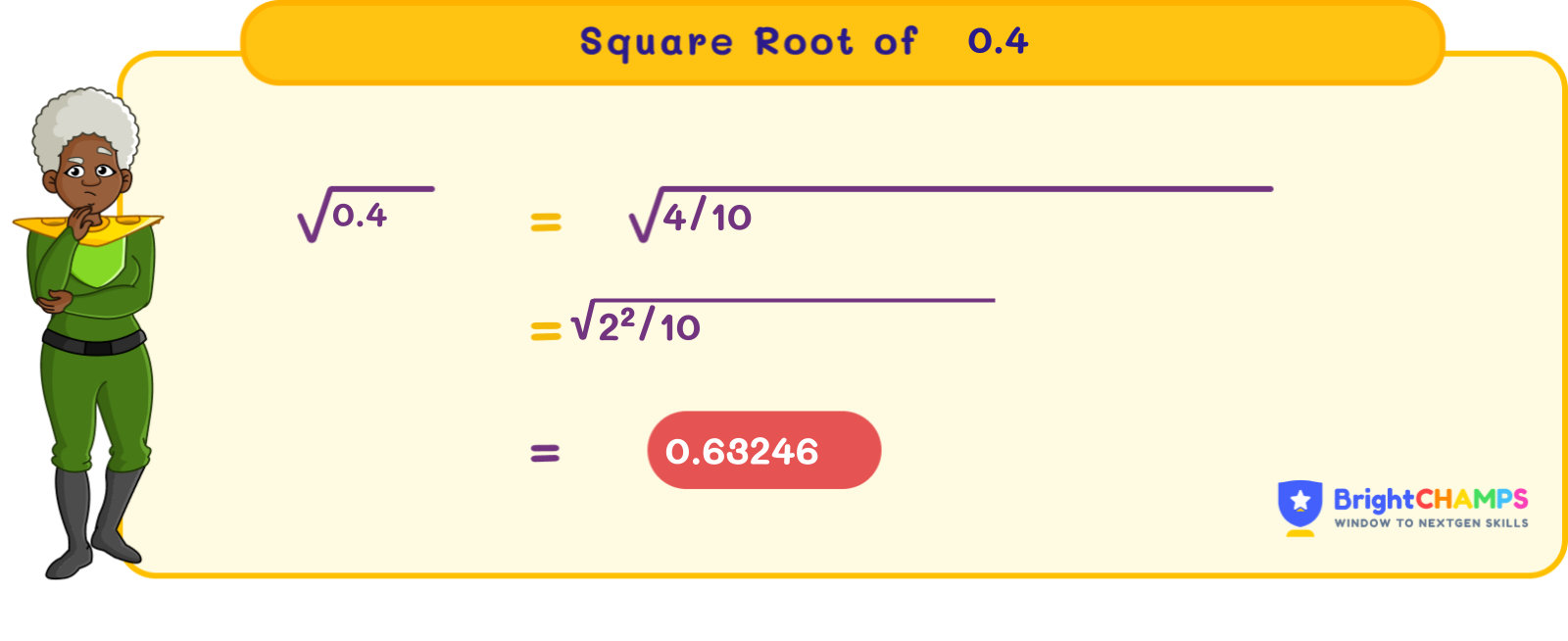
The square root is the inverse of the square of the number. 0.4 is not a perfect square. The square root of 0.4 is expressed in both radical and exponential forms. In the radical form, it is expressed as √0.4, whereas (0.4)^(1/2) in the exponential form. √0.4 = 0.63246, which is an irrational number because it cannot be expressed in the form of p/q, where p and q are integers and q ≠ 0.

The prime factorization method is used for perfect square numbers. However, for non-perfect square numbers, the long-division method and approximation method are used. Let us now learn the following methods:

• Long division method
• Approximation method

The long division method is particularly used for non-perfect square numbers. In this method, we should check the closest perfect square number for the given number. Let us now learn how to find the square root using the long division method, step by step.

Step 1: Start by setting up the number in pairs of two digits from right to left. For 0.4, consider it as 40 (thinking in terms of hundredths).

Step 2: Find a number whose square is less than or equal to 40. The number is 6 because 6 x 6 = 36, which is less than 40.

Step 3: Subtract 36 from 40, the remainder is 4. Bring down two zeros to make it 400.

Step 4: Double the quotient (6) to get 12 and find a number x such that 12x multiplied by x is less than or equal to 400. The number is 3 because 123 x 3 = 369.

Step 5: Subtract 369 from 400, the remainder is 31. Continue this process to get additional decimal places.

So, the square root of √0.4 is approximately 0.632.

The approximation method is another way to find square roots; it is an easy method for estimating the square root of a given number. Now let us learn how to find the square root of 0.4 using the approximation method.

Step 1: Identify the closest perfect squares around √0.4. For 0.4, the nearest perfect squares are 0.36 (which is 0.6²) and 0.49 (which is 0.7²). √0.4 falls between 0.6 and 0.7.

Step 2: Use interpolation to approximate the value. Using interpolation, we estimate √0.4 ≈ 0.632.

• Square root: A square root is the inverse of a square. Example: 0.6² = 0.36, and the inverse of the square is the square root, which is √0.36 = 0.6.
   
• Irrational number: An irrational number is a number that cannot be written in the form p/q, where q is not equal to zero and p and q are integers.
   
• Principal square root: A number has both positive and negative square roots; however, it is always the positive square root that is more prominently used in the real world. That is why it is also known as the principal square root.
   
• Decimal: A decimal is a number that has a whole number and a fraction in a single number, for example, 0.4, 0.632, and 1.57.
   
• Interpolation: A method used to estimate unknown values that fall between known values, particularly useful for estimating square roots.